取得一个整型变量二进制表示的最后一个「1」

在实际工作中，我需要取得一个整数二进制表示的最后一个「1」在哪里。

最朴素的办法，是用短除法，逐次取余数。高明一点的办法，可以是将目标整数向右逐次右移 1 位，然后与常数 1 按位取与，结合计数器判断「1」的位置。

这里，我们介绍一个更加「聪明」的办法。

原码、反码和补码

原码、反码和补码，是讨论整数在计算机中存储方式时用到的术语。

原码最好理解，对人类来说最直观。原码用最高位（最左边的二进制位）表示正负号，余下的部分表示数值。比如：

1 2	20 = 0001 0100(原) -20 = 1001 0100(原)

对于正数来说，其反码和原码一致。对负数来说，反码就是对除去最高符号位之外的所有二进制位取反。比如：

1 2	20 = 0001 0100(原) = 0001 0100(反) -20 = 1001 0100(原) = 1110 1011(反)

对于正数来说，其补码与反码一致。对负数来说，补码就是对反码做通常意义上的加一操作（含进位）。比如：

1 2	20 = 0001 0100(原) = 0001 0100(反) = 0001 0100(补) -20 = 1001 0100(原) = 1110 1011(反) = 1110 1100(补)

整数在计算机中是以补码的形式储存的，这就是为什么我们要介绍原码、反码和补码。补码的好处，其一是明确了整数「0」的表示（否则可以有 0000 0000 和 1000 0000 两种方式表示），其二是对整数的加法只需要统一的一套电路来处理即可。

一点观察

1 2	20 = 0001 0100(补) -20 = 1110 1100(补)

在上面的例子中，我们注意到两个事实：

20 的最后一个非零二进制位是倒数第三位（0100），-20 的最后一个非零二进制位也恰好是倒数第三位（1100）。
从倒数第四位开始往前，20 和 -20 的二进制补码，一一对应，两两互补。

这样一来，很容易看出：

1	0000 0100(补) = 4 = 20 & -20 = 0001 0100(补) & 1110 1100(补)

也就是说，20 与其相反数按位取与，就得到了它二进制表示的最后一个「1」；同理，-20 与其相反数按位取于，也能得到想要的结果。

这是一个普遍规律吗？让我们多看几个例子。

1
2
3

0000 0010(补) = 2 = 54 & -54 = 0011 0110(补) & 1100 1010(补)
0000 0001(补) = 1 = 11 & -11 = 0000 1011(补) & 1111 0101(补)
0100 0000(补) = 64 = 64 & -64 = 0100 0000(补) & 1100 0000(补)

毫无例外，测试的三个整数，都符合我们发现的规律。看起来，这会是一个普遍的规律，因此我们考虑来证明它。

规律的证明

现在我们要去证明：任何整数，其二进制补码表示的最后一个「1」，可由该整数与其相反数按位取与得到。

零的处理

零的二进制补码：

1 2	0 = 0000 0000(原) = 0000 0000(反) = 0000 0000(补) -0 = 0 = 0000 0000(原) = 0000 0000(反) = 0000 0000(补)

显然，0 & -0 = 0，说明 0 的二进制表示中没有 1。因此结论对 0 成立。

非零的处理

命题是对偶的。显然，如果证明了命题对正整数成立，那么对负整数也成立。因此，我们只需要考虑正整数的情况。

现假设，一个正整数二进制表示的最低 k 位均为 0，也就是：

1	0(高位部分)1(k 个 0)

那么，其相反数的反码则是：

1	1(高位部分按位取反)0(k 个 1)

按照补码的定义，对相反数的反码做通常意义上的二进制加一操作，注意低位逐次进位，得到：

1	1(高位部分按位取反)1(k 个 0)

注意到 0 & 0 = 0 & 1 = 1 & 0 = 0，所以除了二进制表示中最后一个「1」，在相反数按位取与之后，所有的二进制位都是零。

这样一来，我们就证明了结论。

Cpp 实现

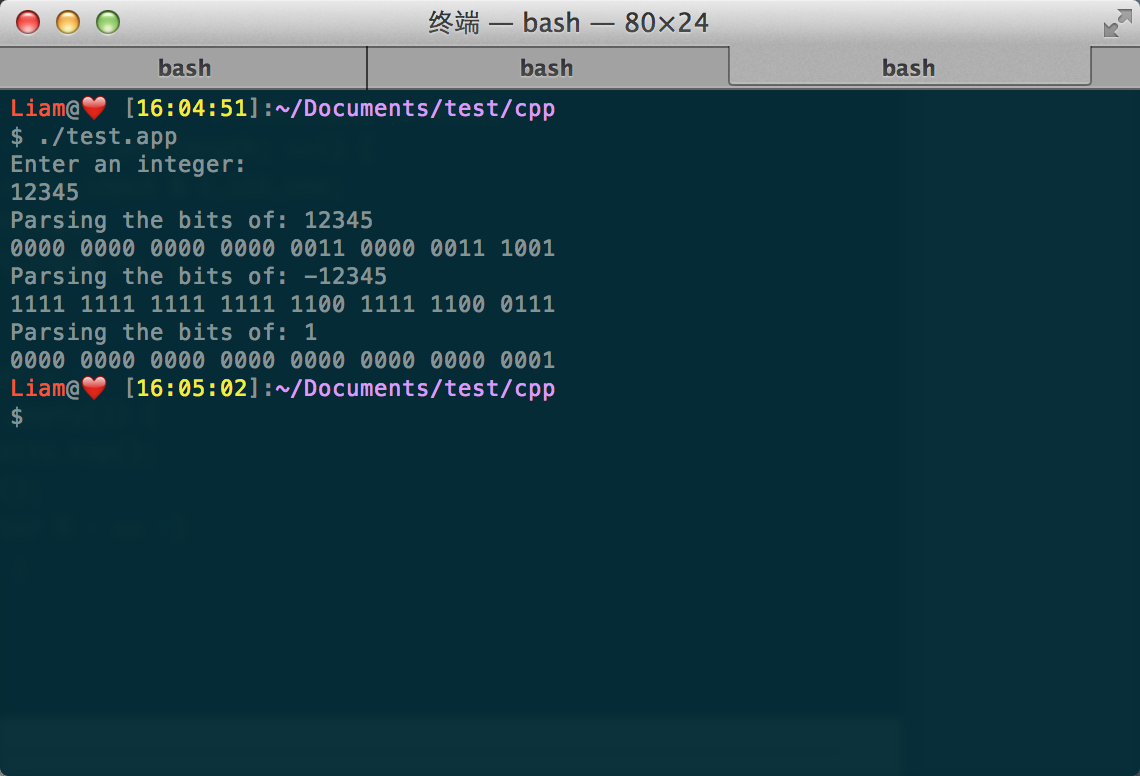
简单用 Cpp 实现了一个测试小工具，用来验证上面的结论：

#include <iostream>
#include <stack>

using namespace std;

int main () {
    int int_wk;
    cout << "Enter an integer:" << endl;
    cin >> int_wk;

    void printBits (int int_input);

    printBits(int_wk);
    printBits(-int_wk);
    printBits((int_wk & -int_wk));

    return 0;
}

void printBits (int int_input) {
    unsigned uns_length = 8 * sizeof(int_input);
    stack<int> stack_bits;
    const int c_int_one = 1;

    cout << "Parsing the bits of: " << int_input << endl;
    for (unsigned i = 0; i != uns_length; ++i) {
        const int tmp = int_input & c_int_one;
        stack_bits.push(tmp);
        int_input = int_input >> 1;
    }

    unsigned uns_counter = 0;
    while (!stack_bits.empty()) {
        cout << stack_bits.top();
        stack_bits.pop();
        if (++uns_counter % 4 == 0)
            cout << " ";
    }
    cout << endl;
}