谈谈利用竖式手工开平方

前段时间，在知乎上看到有人将「手工开平方」列为失传的技艺。本宝宝表示不服，今天来讲讲竖式开平方的原理和操作方法。

原理

简便起见，我们假设有

$$\bigl(\alpha\beta_{(10)}\bigr)^2 = abcd_{(10)}.$$

其中 $\alpha\beta_{(10)}$ 表示它是一个十进制数；而 $\alpha\beta$ 则表示 $\alpha\cdot\beta$ 。我们将 $\alpha\beta_{(10)}$ 按进制位拆开：

$$\alpha\beta_{(10)} = \alpha * 10^1 + \beta * 10^0$$

那么有：

$$abcd_{(10)} = \alpha^2 * 10^{2 * 1} + 2\alpha\beta* 10^{1 + 0} + \beta^2* 10^{2 * 0}$$

从这个分析中，我们可以看出来个简单的规律：

\begin{equation} \label{sum-square} (\alpha + \beta) ^ {2} = \alpha ^ {2} + 2\alpha\beta + \beta ^ {2} \end{equation}

所以，手工开平方的原理，可以简单概括为：从低位开始往高位，两位两位地分割；再从高位往低位，利用和平方公式，逐位地确定平方根。

举个栗子，假设我们要求 $144$ 的平方根（虽然我们都知道是 $12$）。

首先，我们从低位往高位，两位两位地分割，得到 $1$, $44$。注意，这里的 $1$ 指的是 $1 * 10^2$。由于平方数的高位，完全决定平方根的高位。又有：

$$ \begin{cases} 1^2 = 1,\\ 2^2 = 4 > 1. \end{cases} $$

所以，我们确定平方根的高位是 $1$。这也就是说，在公式 \ref{sum-square} 中，我们已经确定 $\alpha = 1 * 10^1 = 10$。现在要求解，满足下式的最大的整数 $\beta$。

$$2 * \alpha * \beta + \beta ^ {2} \leqslant 44 = 144 - 10^2,$$

这也就是

\begin{equation} \label{getting-b} (2 * \alpha + \beta) * \beta \leqslant 44. \end{equation}

显然，$\beta = 2$ 时，式 \ref{getting-b} 的等号成立。这说明，$144 = (10 + 2)^2 = 12^2$。

通过上面的原理分析和举例说明，我们不难得到一个 step-by-step 的操作方法。详述如下：

对平方数，从小数点开始，两位两位地向两端划分（向整数部分的高位和小数部分的低位）；
对最高位的分割，假设为 $ab_{(10)}$ ，求最大的整数 $\alpha$ ，满足 $\alpha^2 \leqslant ab_{(10)}$ ；
求余数 $\overline{cd}_{(10)} = abcd_{(10)} - \alpha^2 * 10^2$ ；
求最大的整数 $\beta$ ，满足 $(2 * \alpha + \beta) * \beta \leqslant \overline{cd}_{(10)}$ ；
类似地方法，依次往低位运算，直到求得平方根，或达成目标精度为止。

下面我们通过一个例子，用竖式的方式，遵照上面的步骤，手工开平方根。

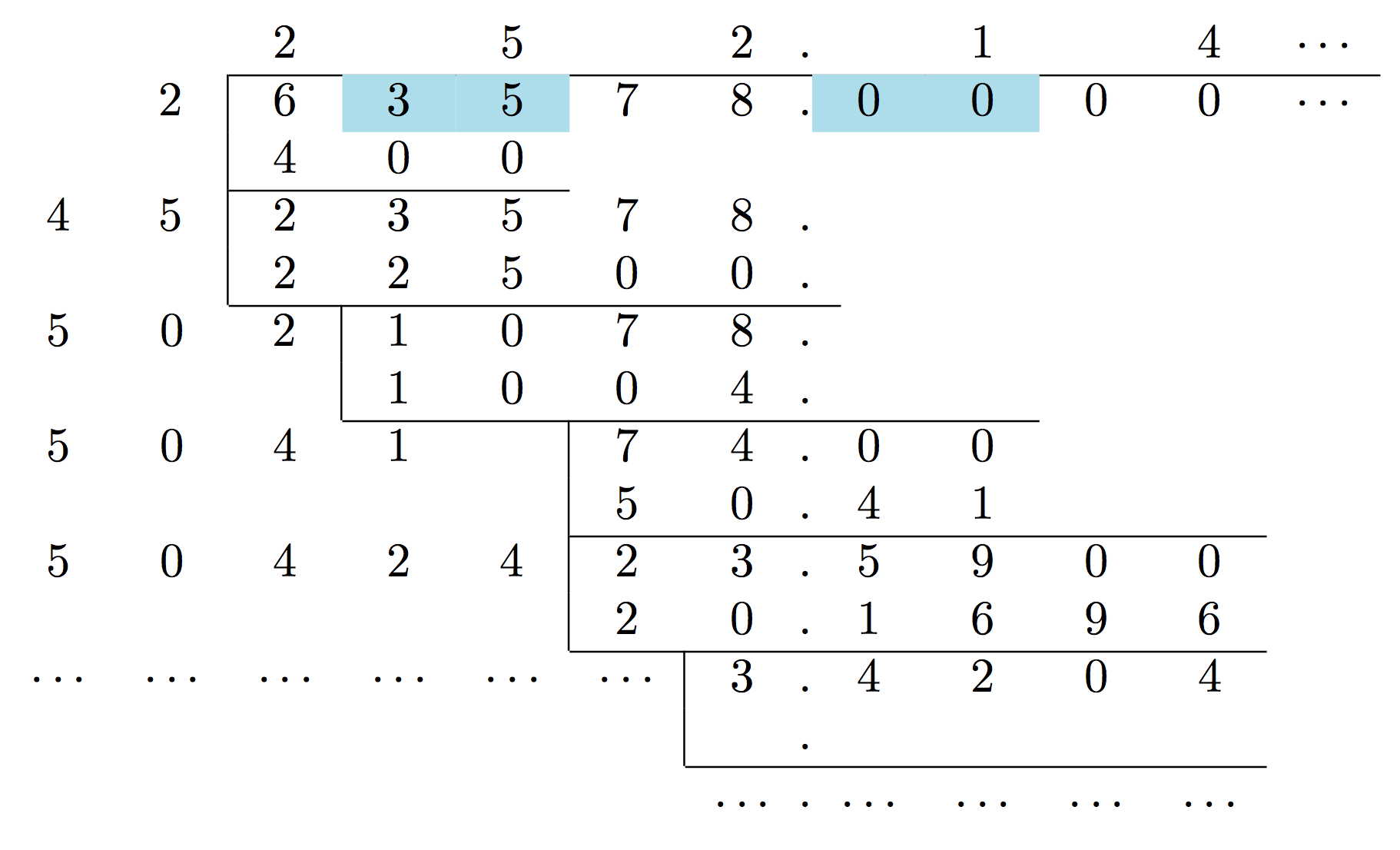
首先，考察高位 $6$。我们有 $2^2 \leqslant 6$ 但 $(2 + 1)^2 > 6$。所以平方根首位是 $2$。

接下来，求余数，得 $235$，这就是上述步骤中的 $\overline{cd}_{(10)}$ 。$2$ 翻倍为 $4$，我们要找满足 $4\beta_{(10)} * \beta \leqslant 235$ 的最大的 $\beta$。求得结果是 $\beta = 5$。

重复地，求余数，得 $1078$。$25$ 翻倍为 $50$，我们要找满足 $50\beta_{(10)} * \beta \leqslant 1078$ 的最大的 $\beta$。求得结果是 $\beta = 2$。

重复地，求余数，得 $7400$。$252$ 翻倍为 $504$，我们要找满足 $504\beta_{(10)} * \beta \leqslant 7400$ 的最大的 $\beta$。求得结果是 $\beta = 1$。

重复地，求余数，得 $235900$。$2521$ 翻倍为 $5042$，我们要找满足 $5042\beta_{(10)} * \beta \leqslant 235900$ 的最大的 $\beta$。求得结果是 $\beta = 4$。

……

如此重复，可以求得更高的精度。不过，作为演示，这个例子就到此为止了。我们得到结果 $\sqrt{63578} = 252.14\cdots$。