本篇基本上是原作的翻译。转载请保留本段文字。
复杂度通常会使用大-O 记号来表示,比如快速排序的平均时间复杂度是 $O(n \log(n))$。虽然我是「理解派」,但是虽然每个算法/数据结构都理解了,不时仍有可能忘记具体某个算法/数据结构的复杂度(特别是在最好、最坏和平均情形下的复杂度)。因此制作一个速查表是蛮有必要的。
动手前先看看是否已经有轮子是一个好习惯,果不其然,我找到了原作。
图例
抽象数据结构的操作复杂度
| 数据结构 | 时间复杂度 | 空间复杂度 |
|---|
| | 平均 | 最差 | 最差 |
|---|
| | 访问 | 搜索 | 插入 | 删除 | 访问 | 搜索 | 插入 | 删除 | |
|---|
| 顺序表 | $O(1)$ | $O(n)$ | $O(n)$ | $O(n)$ | $O(1)$ | $O(n)$ | $O(n)$ | $O(n)$ | $O(n)$ |
| 栈 | $O(n)$ | $O(n)$ | $O(1)$ | $O(1)$ | $O(n)$ | $O(n)$ | $O(1)$ | $O(1)$ | $O(n)$ |
| 单链表 | $O(n)$ | $O(n)$ | $O(1)$ | $O(1)$ | $O(n)$ | $O(n)$ | $O(1)$ | $O(1)$ | $O(n)$ |
| 双链表 | $O(n)$ | $O(n)$ | $O(1)$ | $O(1)$ | $O(n)$ | $O(n)$ | $O(1)$ | $O(1)$ | $O(n)$ |
| 跳表 | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(n)$ | $O(n)$ | $O(n)$ | $O(n)$ | $O(n \log(n))$ |
| 散列表 | - | $O(1)$ | $O(1)$ | $O(1)$ | - | $O(n)$ | $O(n)$ | $O(n)$ | $O(n)$ |
| 二叉搜索树 | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(n)$ | $O(n)$ | $O(n)$ | $O(n)$ | $O(n)$ |
| 笛卡尔树 | - | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | - | $O(n)$ | $O(n)$ | $O(n)$ | $O(n)$ |
| B-树 | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(n)$ |
| 红黑树 | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(n)$ |
| 伸展树 | - | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | - | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(n)$ |
| AVL 树 | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(n)$ |
数组排序
| 算法 | 时间复杂度 | 空间复杂度 |
|---|
| | 最佳 | 平均 | 最差 | 最差 |
|---|
| 快速排序 | $O(n \log(n))$ | $O(n \log(n))$ | $O(n^2)$ | $O(\log(n))$ |
| 归并排序 | $O(n \log(n))$ | $O(n \log(n))$ | $O(n \log(n))$ | $O(n)$ |
| Timsort | $O(n)$ | $O(n \log(n))$ | $O(n \log(n))$ | $O(n)$ |
| 堆排序 | $O(n \log(n))$ | $O(n \log(n))$ | $O(n \log(n))$ | $O(1)$ |
| 冒泡排序 | $O(n)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ |
| 插入排序 | $O(n)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ |
| 选择排序 | $O(n^2)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ |
| 希尔排序 | $O(n)$ | $O((n\log(n))^2)$ | $O((n\log(n))^2)$ | $O(1)$ |
| 桶排序 | $O(n+k)$ | $O(n+k)$ | $O(n^2)$ | $O(n)$ |
| 基数排序 | $O(nk)$ | $O(nk)$ | $O(nk)$ | $O(n+k)$ |
图操作
| 节点 / 边界管理 | 存储 | 增加顶点 | 增加边界 | 移除顶点 | 移除边界 | 查询 |
|---|
| 邻接表 | $O(|V|+|E|)$ | $O(1)$ | $O(1)$ | $O(|V| + |E|)$ | $O(|E|)$ | $O(|V|)$ |
| 邻接矩阵 | $O(|V|^2)$ | $O(|V|^2)$ | $O(1)$ | $O(|V|^2)$ | $O(1)$ | $O(1)$ |
堆操作
| 类型 | 时间复杂度 |
|---|
| | 建堆 | 查找最大值 | 分离最大值 | 提升键 | 插入 | 删除 | 合并 |
|---|
| (排好序的)链表 | - | $O(1)$ | $O(1)$ | $O(n)$ | $O(n)$ | $O(1)$ | $O(m+n)$ |
| (未排序的)链表 | - | $O(n)$ | $O(n)$ | $O(1)$ | $O(1)$ | $O(1)$ | $O(1)$ |
| 二叉堆 | $O(n)$ | $O(1)$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(\log(n))$ | $O(m+n)$ |
| 二项堆 | - | $O(1)$ | $O(\log(n))$ | $O(\log(n))$ | $O(1)$ | $O(\log(n))$ | $O(\log(n))$ |
| 斐波那契堆 | - | $O(1)$ | $O(\log(n))$ | $O(1)$ | $O(1)$ | $O(\log(n))$ | $O(1)$ |
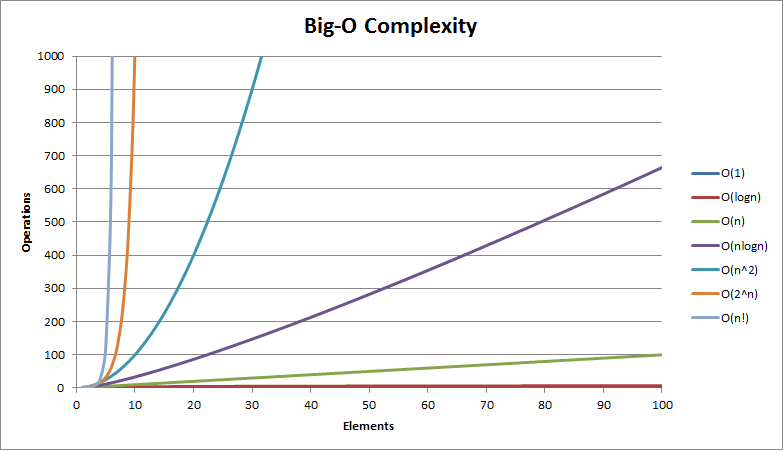
大-O 复杂度曲线
![]()