近日在知乎上看到一则和应聘/面试有关的小故事。题主提到,面试官请他计算 sin 36° 的值。
这里我们用几种办法来计算。
纯代数方法
考虑 $\sin 36^\circ = 2\sin 18^\circ\cos 18^\circ$,如果我们有办法求得 $18^\circ$ 的正弦值或余弦值,我们就能根据二倍角公式,直接得到 $36^\circ$ 的正弦值。
考虑 $\sin 54^\circ = \cos 36^\circ$,而有
\begin{equation} \begin{aligned} \sin 54^\circ &{}= 3\sin 18^\circ - 4\sin^3 18^\circ\\ \cos 36^\circ &{}= 1 - 2\sin^2 18^\circ \end{aligned} \end{equation}
我们能得到关于 $\sin 18^\circ$ 的方程
\begin{equation} 4x^3 - 2x^2 - 3x + 1 = 0 \end{equation}
作因式分解,也就是
\begin{equation} (x - 1)(4x^2 + 2x - 1) = 0 \end{equation}
该方程有 3 个解,考虑 $\sin 18^\circ \in (0, 1)$,取有效解 $\sin 18^\circ = \frac{\sqrt{5} - 1}{4}$。如此容易求得 $\sin 36^\circ = \frac{\sqrt{10 - 2\sqrt{5}}}{4}$。
借助黄金三角形和正弦定理
作等腰 $\triangle ABC$,其中 $\angle CAB = 36^\circ$, $\angle ABC = \angle BCA = 72^\circ$。记底边长度 $\overline{BC} = a$,记腰长 $\overline{AB} = \overline{CA} = b$。
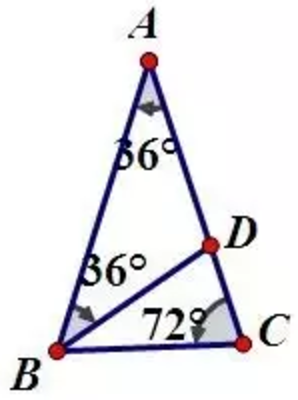
过 $B$ 做 $\angle ABC$ 的角平分线,与边 $CA$ 交于点 $D$。如此,图中有 3 个等腰三角形:$\triangle ABC$, $\triangle BCD$, $\triangle DAB$。并且,显而易见地有 $\triangle ABC \sim \triangle BCD$。
考虑等腰,有 $\frac{\overline{BC}}{\overline{CD}} = \frac{\overline{AB}}{\overline{BC}}$。这也就是说
\begin{equation}\overline{CD} = \frac{a^2}{b},\end{equation}
因此
\begin{equation}\overline{DA} = b - \frac{a^2}{b}.\end{equation}
考虑等腰,有 $\overline{BC} = \overline{BD} = \overline{DA}$,所以
\begin{equation}a = b - \frac{a^2}{b},\end{equation}
也就是
\begin{equation}\biggl(\frac{b}{a}\biggr)^2 - \frac{b}{a} - 1 = 0.\end{equation}
取有效解,知 $\frac{b}{a} = \frac{\sqrt{5} + 1}{2}$。在 $\triangle ABC$ 中应用正弦定理,有
\begin{equation}\frac{\sin 72^\circ}{\sin 36^\circ} = \frac{2\sin 36^\circ\cos 36^\circ}{\sin 36^\circ} = \frac{b}{a} = 2\cos 36^\circ = \frac{\sqrt{5} + 1}{2},\end{equation}
知 $\cos 36^\circ = \frac{\sqrt{5} + 1}{4}$,易得 $\sin 36^\circ = \frac{\sqrt{10 - 2\sqrt{5}}}{4}$。


