始终

不忘初心

0%

谈谈 Bias-Variance Tradeoff

发表于 更新于 分类于
本文字数： 5.9k 阅读时长 ≈ 11 分钟

准确是两个概念。准是 bias 小，确是 variance 小。准确是相对概念，因为 bias-variance tradeoff。
——Liam Huang

在机器学习领域，人们总是希望使自己的模型尽可能准确地描述数据背后的真实规律。通俗所言的「准确」，其实就是误差小。在领域中，排除人为失误，人们一般会遇到三种误差来源：随机误差、偏差和方差。偏差和方差又与「欠拟合」及「过拟合」紧紧联系在一起。由于随机误差是不可消除的，所以此篇我们讨论在偏差和方差之间的权衡（Bias-Variance Tradeoff）。

定义

数学上定义

首先需要说明的是随机误差。随机误差是数据本身的噪音带来的，这种误差是不可避免的。一般认为随机误差服从高斯分布，记作 $\epsilon\sim\mathcal N(0, \sigma_\epsilon)$。因此，若有变量 $y$ 作为预测值，以及 $X$ 作为自变量（协变量），那么我们将数据背后的真实规律 $f$ 记作

$$y = f(X) + \epsilon.$$

偏差和方差则需要在统计上做对应的定义。

  • 偏差（bias）描述的是通过学习拟合出来的结果之期望，与真实规律之间的差距，记作 $\text{Bias}(X) = E[\hat f(X)] - f(X)$。
  • 方差（variance）即是统计学中的定义，描述的是通过学习拟合出来的结果自身的不稳定性，记作 $\text{Var}(X) = E\Bigl[\bigl(\hat f(X) - E[\hat f(X)]\bigr)^{2}\Bigr]$。

以均方误差为例，有如下推论

\begin{equation} \begin{aligned} \text{Err}(X) &{}= E\Bigl[\bigl(y - \hat f(X)\bigr)^2\Bigr] \\ &{}= E\Bigl[\bigl(f(X) + \epsilon - \hat f(X)\bigr)^2\Bigr] \\ &{}= \left(E[\hat{f}(X)]-f(X)\right)^2 + E\left[\left(\hat{f}(X)-E[\hat{f}(X)]\right)^2\right] +\sigma_\epsilon^2 \\ &{}= \text{Bias}^2 + \text{Variance} + \text{Random Error}. \end{aligned} \label{eq:err-comp} \end{equation}

直观的图示

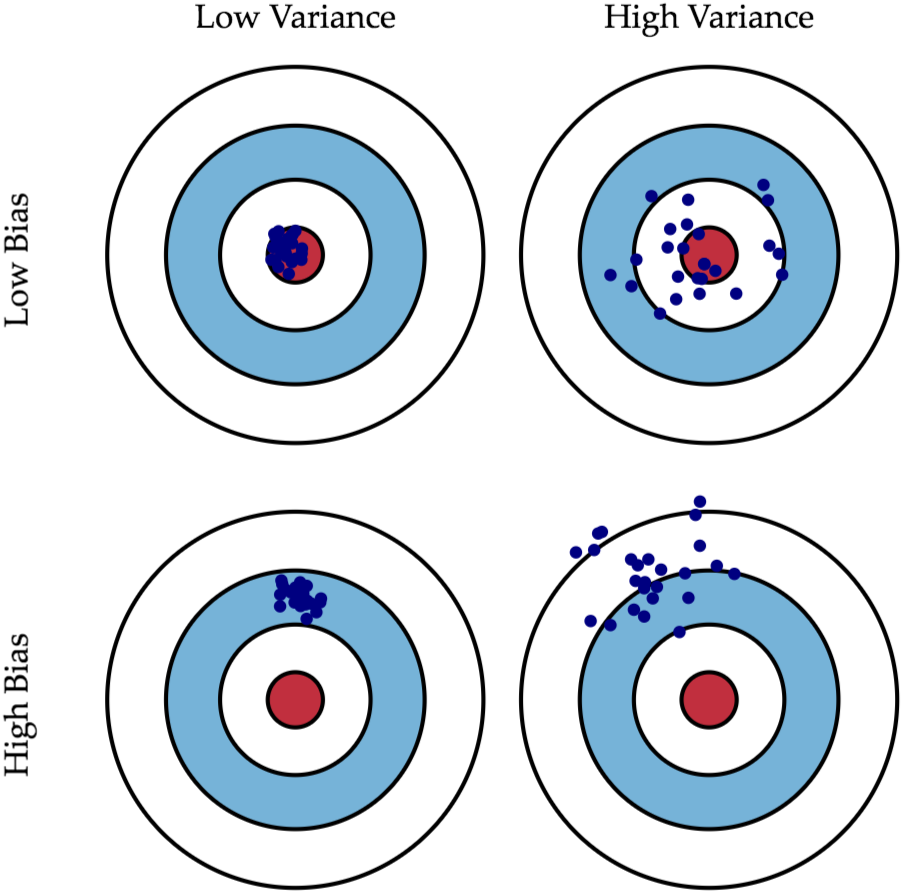
下图将机器学习任务描述为一个「打靶」的活动：根据相同算法、不同数据集训练出的模型，对同一个样本进行预测；每个模型作出的预测相当于是一次打靶。


http://scott.fortmann-roe.com/docs/BiasVariance.html

左上角的示例是理想状况：偏差和方差都非常小。如果有无穷的训练数据，以及完美的模型算法，我们是有办法达成这样的情况的。然而，现实中的工程问题，通常数据量是有限的，而模型也是不完美的。因此，这只是一个理想状况。

右上角的示例表示偏差小而方差大。靶纸上的落点都集中分布在红心周围，它们的期望落在红心之内，因此偏差较小。另外一方面，落点虽然集中在红心周围，但是比较分散，这是方差大的表现。

左下角的示例表示偏差大二方差小。显而易见，靶纸上的落点非常集中，说明方差小。但是落点集中的位置距离红心很远，这是偏差大的表现。

右下角的示例则是最糟糕的情况，偏差和方差都非常大。这是我们最不希望看到的结果。

举个栗子

现在我们做一个模拟实验，用以说明至此介绍的内容。

首先，我们生成了两组 array，分别作为训练集和验证集。这里，x 与 y 是接近线性相关的，而在 y 上加入了随机噪声，用以模拟真实问题中的情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
import numpy as np
np.random.seed(42)  # the answer to life, the universe and everything
real = lambda x:x + x ** 0.1

x_train = np.linspace(0, 15, 100)
y_train = map(real, x_train)
y_noise = 2 * np.random.normal(size = x_train.size)
y_train = y_train + y_noise

x_valid = np.linspace(0, 15, 50)
y_valid = map(real, x_valid)
y_noise = 2 * np.random.normal(size = x_valid.size)
y_valid = y_valid + y_noise

现在，我们选用最小平方误差作为损失函数，尝试用多项式函数去拟合这些数据。

1
2
3
4
prop    = np.polyfit(x_train, y_train, 1)
prop_   = np.poly1d(prop)
overf   = np.polyfit(x_train, y_train, 15)
overf_  = np.poly1d(overf)

这里，对于 prop，我们采用了一阶的多项式函数（线性模型）去拟合数据；对于 overf，我们采用了 15 阶的多项式函数（多项式模型）去拟合数据。如此，我们可以把拟合效果绘制成图。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import matplotlib.pyplot as plt

_ = plt.figure(figsize = (14, 6))

plt.subplot(1, 2, 1)
prop_e  = np.mean((y_train - np.polyval(prop, x_train)) ** 2)
overf_e = np.mean((y_train - np.polyval(overf, x_train)) ** 2)
xp      = np.linspace(-2, 17, 200)
plt.plot(x_train, y_train, '.')
plt.plot(xp, prop_(xp), '-', label = 'proper, err: %.3f' % (prop_e))
plt.plot(xp, overf_(xp), '--', label = 'overfit, err: %.3f' % (overf_e))
plt.ylim(-5, 20)
plt.legend()
plt.title('train set')

plt.subplot(1, 2, 2)
prop_e  = np.mean((y_valid - np.polyval(prop,  x_valid)) ** 2)
overf_e = np.mean((y_valid - np.polyval(overf, x_valid)) ** 2)
xp      = np.linspace(-2, 17, 200)
plt.plot(x_valid, y_valid, '.')
plt.plot(xp, prop_(xp), '-', label = 'proper, err: %.3f' % (prop_e))
plt.plot(xp, overf_(xp), '--', label = 'overfit, err: %.3f' % (overf_e))
plt.ylim(-5, 20)
plt.legend()
plt.title('validation set')

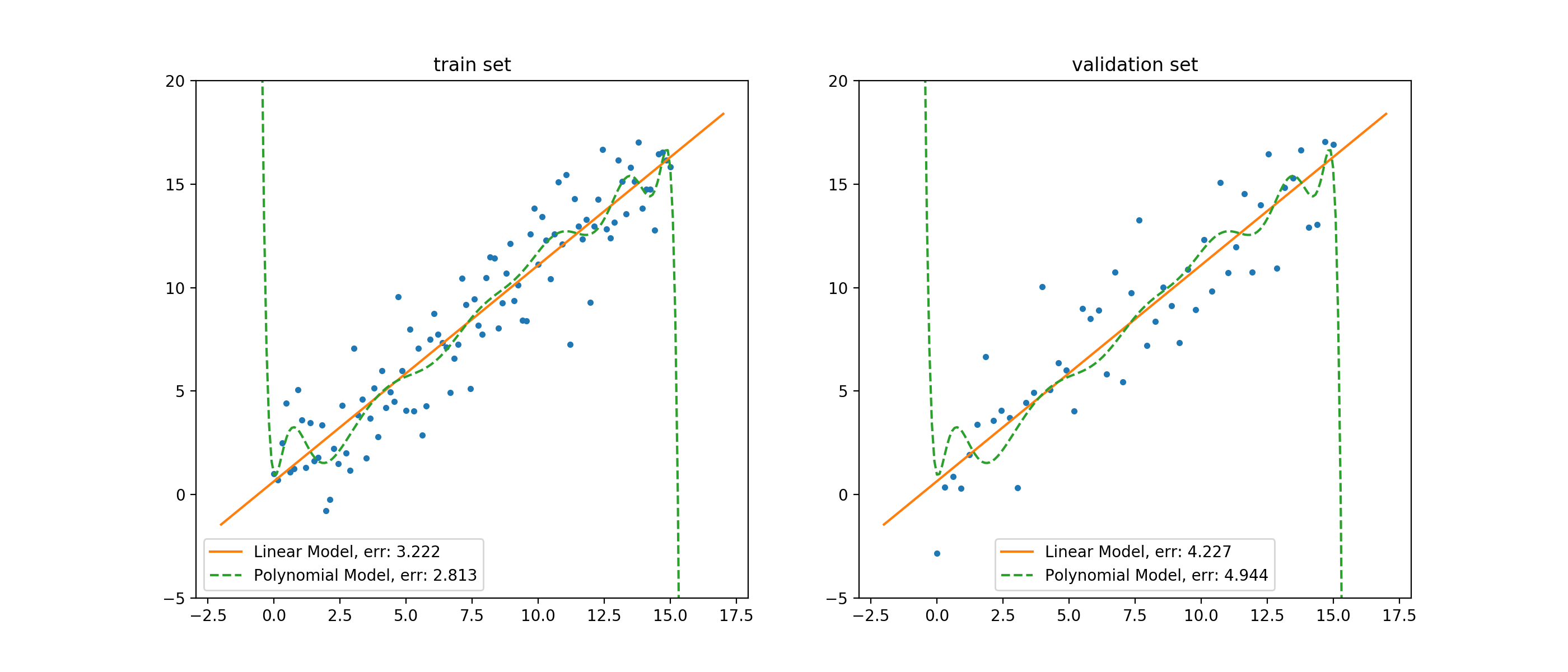
多项式拟合结果

以训练集上的结果来说，线性模型的误差要明显高于多项式模型。站在人类观察者的角度来说，这似乎是显而易见的：数据是围绕一个近似线性的函数附近抖动的，那么用简单的线性模型，自然就无法准确地拟合数据；但是，高阶的多项式函数可以进行各种「扭曲」，以便将训练集的数据拟合得更好。

这种情况，我们说线性模型在训练集上欠拟合（underfitting），并且它的偏差（bias）要高于多项式模型的偏差。

但这并不意味着线性模型在这个问题里，要弱于多项式模型。我们看到，在验证集上，线性模型的误差要小于多项式模型的误差。并且，线性模型在训练集和验证集上的误差相对接近，而多项式模型在两个数据集上的误差，差距就很大了。

这种情况，我们说多项式模型在训练集上过拟合（overfitting），并且它的方差（variance）要高于线性模型的偏差。此外，因为线性模型在两个集合上的误差较为接近，因此我们说线性模型在训练过程中未见的数据上，泛化能力更好。因为，在真实情况下，我们都需要使用有限的训练集去拟合模型，而后工作在无限的真实样本中，而这些真实样本对于模型训练过程都是不可见的。所以，模型的泛化能力，是非常重要的指标。

考虑到两个模型在验证集上的表现，在这个任务上，我们说线性模型表现得较好。

权衡之术

克服 OCD

对于很多人来说，不可避免地会有这样的强迫症：希望训练误差降至 0。

我们说，人想要过得快乐，首先要接纳自己，与自己和解。做机器学习相关的任务也是一样，首先要理解和接受机器学习的基本规律，克服自己的强迫症。

首先，对于误差，在公式 \ref{eq:err-comp} 中，我们得知误差中至少有「随机误差」是无论如何不可避免的。因此，哪怕有一个模型在训练集上的表现非常优秀，它的误差是 0，这也不能说明这个模型完美无缺。因为，训练集本身存在的误差，将会被带入到模型之中；也就是说，这个模型天然地就和真实情况存在误差，于是它不是完美的。

其次，由于训练样本无法完美地反应真实情况（样本容量有限、抽样不均匀），以及由于模型本身的学习能力存在上限，也意味着我们的模型不可能是完美的。

因此，我们需要克服强迫症，不去追求训练误差为 0；转而去追求在给定数据集和模型算法的前提下的，逼近最优结果。

最佳平衡点的数学表述

在实际应用中，我们做模型选择的一般方法是：

  • 选定一个算法；
  • 调整算法的超参数；
  • 以某种指标选择最合适的超参数组合。

也就是说，在整个过程中，我们固定训练样本，改变模型的描述能力（模型复杂度）。不难理解，随着模型复杂度的增加，其描述能力也就会增加；此时，模型在验证集上的表现，偏差会倾向于减小而方差会倾向于增大。而在相反方向，随着模型复杂度的降低，其描述能力也就会降低；此时，模型在验证集上的表现，偏差会倾向于增大而方差会倾向于减小。

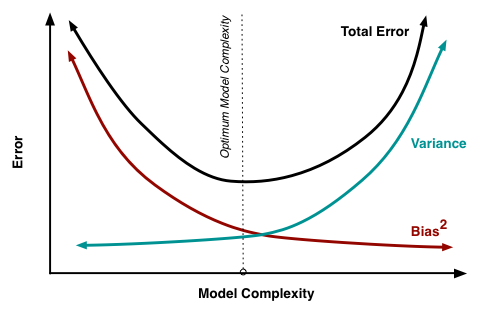
考虑到，模型误差是偏差与方差的加和，因此我们可以绘制出这样的图像。

偏差与误差的变化趋势
http://scott.fortmann-roe.com/docs/BiasVariance.html

图中的最优位置，实际上是 total error 曲线的拐点。我们知道，连续函数的拐点意味着此处一阶导数的值为 0。考虑到 total error 是偏差与方差的加和，所以我们有，在拐点处：

\begin{equation} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \frac{\dif\text{Bias}}{\dif\text{Complexity}} = - \frac{\dif\text{Variance}}{\dif\text{Complexity}} \label{eq:sweet} \end{equation}

公式 \ref{eq:sweet} 给出了寻找最优平衡点的数学描述。若模型复杂度大于平衡点，则模型的方差会偏高，模型倾向于过拟合；若模型复杂度小于平衡点，则模型的偏差会偏高，模型倾向于欠拟合。

过拟合与欠拟合的外在表现

尽管有了上述数学表述，但是在现实环境中，有时候我们很难计算模型的偏差与方差。因此，我们需要通过外在表现，判断模型的拟合状态：是欠拟合还是过拟合。

同样地，在有限的训练数据集中，不断增加模型的复杂度，意味着模型会尽可能多地降低在训练集上的误差。因此，在训练集上，不断增加模型的复杂度，训练集上的误差会一直下降。

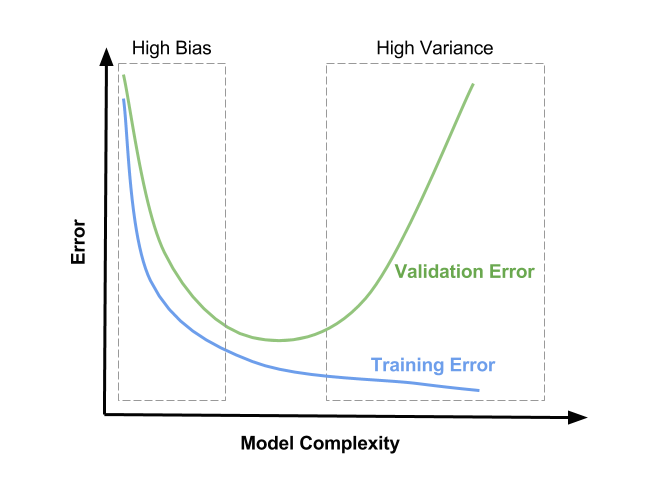
因此，我们可以绘制出这样的图像。

训练集和验证集上的误差变化
http://www.learnopencv.com/bias-variance-tradeoff-in-machine-learning/

因此，

  • 当模型处于欠拟合状态时，训练集和验证集上的误差都很高；
  • 当模型处于过拟合状态时，训练集上的误差低，而验证集上的误差会非常高。

处理欠拟合与过拟合

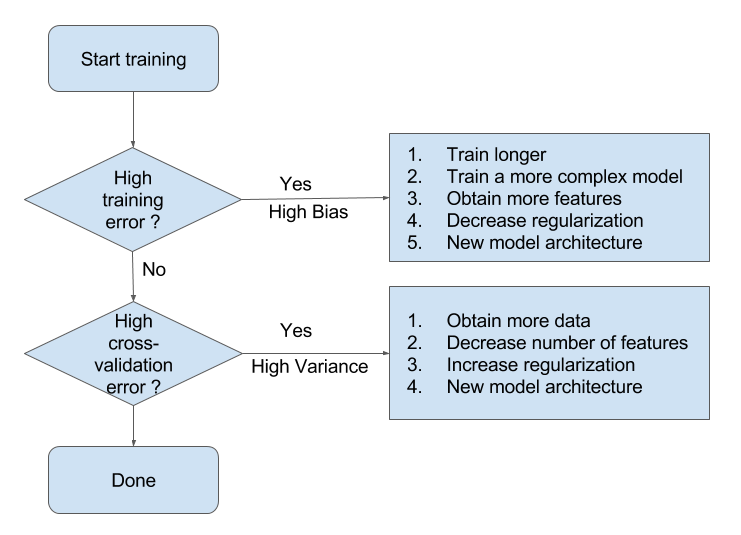
有了这些分析，我们就能比较容易地判断模型所处的拟合状态。接下来，我们就可以参考 Andrew Ng 博士提供的处理模型欠拟合/过拟合的一般方法了。

机器学习调试的一般流程

欠拟合

当模型处于欠拟合状态时，根本的办法是增加模型复杂度。我们一般有以下一些办法：

  • 增加模型的迭代次数；
  • 更换描述能力更强的模型；
  • 生成更多特征供训练使用；
  • 降低正则化水平。

过拟合

当模型处于过拟合状态时，根本的办法是降低模型复杂度。我们则有以下一些武器：

  • 扩增训练集；
  • 减少训练使用的特征的数量；
  • 提高正则化水平。
俗话说，投资效率是最好的投资。 如果您感觉我的文章质量不错，读后收获很大，预计能为您提高 10% 的工作效率，不妨小额捐助我一下，让我有动力继续写出更多好文章。