在前作里,我们讨论了机器学习里的偏差-方差权衡。机器学习里的损失函数(代价函数)可以用来描述模型与上帝真相(ground truth)之间的差距,因此可以解决「偏差」的问题。但是仅有损失函数时,我们无法解决方差的问题,因而会有过拟合风险。
今次我们讨论损失函数的反面——正则项,看看 $L_1$-正则项和 $L_2$-正则项是如何使机器学习模型走出过拟合的泥沼的。
损失函数与目标函数
机器学习的目标,实际上就是找到一个足够好的函数 $F^{*}$ 用以预测真实规律。因此,首先我们要定义什么叫做「好」。
对于样本 $(\vec x, y)$ 来说,在机器学习模型 $F$ 的作用下,有预测值 $\hat y = F(\vec x)$。我们可以定义损失函数 $l(y, \hat y)$,来描述预测值 $\hat y$ 与上帝真相 $y$ 之间的差距。
$$l(y, \hat y) = l(y, F(\vec x)).$$
一般来说,损失函数 $l: \mathbb R\times\mathbb R\mapsto \mathbb R$ 是一个有下确界的函数。当预测值 $\hat y$ 与上帝真相 $y$ 相差不多时,则损失函数的值能接近这个下确界;反之,当预测值 $\hat y$ 与上帝真相 $y$ 差距甚远时,损失函数的值会显著地高于下确界。
因此,在整个训练集上,我们可以把机器学习任务转化为一个最优化问题。我们的目标是在泛函空间内,找到能使得全局损失 $L(F)$ 最小的模型 $F$,作为最终模型 $F^{*}$。
$$ F^{*} = \mathop{\text{arg min}}_{F} E_{y,\,\vec x}\Bigl[l\bigl(y,\,F(\vec x)\bigr)\Bigr] = \mathop{\text{arg min}}_{F}L(F). $$
这样的最优化问题解决了机器学习的大半任务,但是它只考虑了对数据的拟合,而忽视了模型本身的复杂度。因此,它留下了一个显而易见的问题:如何防止模型本身的复杂度过高,导致过拟合?为此,我们需要引入正则项(regularizer)$\gamma\Omega(F),,\gamma > 0$,用来描述模型本身的复杂度。于是我们的最优化目标变为
$$ F^{*} = \mathop{\text{arg min}}_{F}\text{Obj}(F) = \mathop{\text{arg min}}_{F}L(F) + \gamma\Omega(F). $$
其中,$\text{Obj}(F)$ 称为目标函数(Objective Function)。
范数与正则项
所谓范数,就是某种抽象的长度。范数满足通常意义上长度的三个基本性质:
- 非负性:$ \lVert\vec x\rVert\geqslant 0 $;
- 齐次性:$ \lVert c\cdot\vec x\rVert = \lvert c\rvert \cdot \lVert\vec x\rVert$;
- 三角不等式:$ \lVert \vec x + \vec y\rVert \leqslant \lVert\vec x\rVert + \lVert\vec y\rVert$。
在这里,我们需要关注的最主要是范数的「非负性」。我们刚才讲,损失函数通常是一个有下确界的函数。而这个性质保证了我们可以对损失函数做最优化求解。如果我们要保证目标函数依然可以做最优化求解,那么我们就必须让正则项也有一个下界。非负性无疑提供了这样的下界,而且它是一个下确界——由齐次性保证(当 $c = 0$ 时)。
因此,我们说,范数的性质使得它天然地适合作为机器学习的正则项。而范数需要的向量,则是机器学习的学习目标——参数向量。
机器学习中有几个常用的范数,分别是
- $ L_0 $-范数:
$ \lVert\vec x\rVert_0 = \#(i),\; \text{with }i\neq 0 $; - $ L_1 $-范数:
$ \lVert\vec x\rVert_1 = \sum_{i = 1}^{d}\lvert x_i\rvert $; - $ L_2 $-范数:
$ \lVert\vec x\rVert_2 = \Bigl(\sum_{i = 1}^{d}x_i^2\Bigr)^{1/2} $; - $ L_p $-范数:
$ \lVert\vec x\rVert_p = \Bigl(\sum_{i = 1}^{d}x_i^p\Bigr)^{1/p} $; $ L_\infty $-范数:$ \lVert\vec x\rVert_\infty = \lim_{p\to+\infty}\Bigl(\sum_{i = 1}^{d}x_i^p\Bigr)^{1/p} $。
在机器学习中,如果使用了 $\lVert\vec w\rVert_p$ 作为正则项;则我们说,该机器学习任务引入了 $L_p$-正则项。
$L_0$ 与 $L_1$-正则项(LASSO regularizer)
在机器学习里,最简单的学习算法可能是所谓的线性回归模型
$$ F(\vec x; \vec w, b) = \sum_{i = 1}^{n} w_i\cdot x_i + b. $$
我们考虑这样一种普遍的情况,即:预测目标背后的真是规律,可能只和某几个维度的特征有关;而其它维度的特征,要不然作用非常小,要不然纯粹是噪声。在这种情况下,除了这几个维度的特征对应的参数之外,其它维度的参数应该为零。若不然,则当其它维度的特征存在噪音时,模型的行为会发生预期之外的变化,导致过拟合。
于是,我们得到了避免过拟合的第一个思路:使尽可能多的参数为零。为此,最直观地我们可以引入 $L_0$-范数。令$$ \Omega\bigl(F(\vec x;\vec w)\bigr) \overset{\text{def}}{=} \ell_0\frac{\lVert\vec w\rVert_0}{n},\;\ell_0 > 0, $$
这意味着,我们希望绝大多数 $ \vec w $ 的分量为零。
通过引入 $L_0$-正则项,我们实际上引入了一种「惩罚」机制,即:若要增加模型复杂度以加强模型的表达能力降低损失函数,则每次使得一个参数非零,则引入 $\ell_0$ 的惩罚系数。也就是说,如果使得一个参数非零得到的收益(损失函数上的收益)不足 $\ell_0$;那么增加这样的复杂度是得不偿失的。
通过引入 $L_0$-正则项,我们可以使模型稀疏化且易于解释,并且在某种意义上实现了「特征选择」。这看起来很美好,但是 $L_0$-正则项也有绕不过去坎:
- 非连续;
- 非凸;
- 不可求导。
因此,$L_0$-正则项虽好,但是求解这样的最优化问题,难以在多项式时间内找到有效解(NP-Hard 问题)。于是,我们转而考虑 $L_0$-范数最紧的凸放松(tightest convex relaxation):$L_1$-范数。令$$ \Omega\bigl(F(\vec x;\vec w)\bigr) \overset{\text{def}}{=} \ell_1\frac{\lVert\vec w\rVert_1}{n},\;\ell_1 > 0, $$
我们来看一下参数更新的过程,有哪些变化。考虑目标函数$$ \text{Obj}(F) = L(F) + \gamma\cdot\ell_1\frac{\lVert\vec w\rVert_1}{n}, $$
有对参数 $ w_i $ 的偏导数$$ \frac{\partial\text{Obj}}{\partial w_i} = \frac{\partial L}{\partial w_i} + \frac{\gamma\ell_1}{n}\text{sgn}(w_i). $$
因此有参数更新过程$$ w_i\to w'_i \overset{\text{def}}{=} w_i - \eta\frac{\partial L}{\partial w_i} - \eta\frac{\gamma\ell_1}{n}\text{sgn}(w_i). $$
因为 $\eta\frac{\gamma\ell_1}{n} > 0$,所以多出的项 $ \eta\frac{\gamma\ell_1}{n}\text{sgn}(w_i) $ 使得 $ w_i \to 0 $,实现「稀疏化」。
$L_2$-正则项(Ridge Regularizer)
让我们回过头,考虑前作中出现过的多项式模型的例子。它的一般形式是$$ F = \sum_{i = 1}^{n} w_i\cdot x^{i} + b. $$
我们注意到,当多项式模型过拟合时,函数曲线倾向于「靠近」噪声点。这意味着,函数曲线会在噪声点之间来回扭曲跳跃。这也就是说,在某些局部,函数曲线的切线斜率非常高——函数导数的绝对值非常大。对于多项式模型来说,函数导数的绝对值,实际上就是多项式系数的一个线性加和。这也就是说,过拟合的多项式模型,它的参数的绝对值会非常大(至少某几个参数分量的绝对值非常大)。因此,如果我们有办法使得这些参数的值,比较稠密均匀地集中在零附近,就能有效地避免过拟合。
于是我们引入 $L_2$-正则项,令$$ \Omega\bigl(F(\vec x;\vec w)\bigr) \overset{\text{def}}{=} \ell_2\frac{\lVert\vec w\rVert_2^2}{2n},\;\ell_2 > 0, $$
因此有目标函数$$ \text{Obj}(F) = L(F) + \gamma\cdot\ell_2\frac{\lVert\vec w\rVert_2^2}{2n}, $$
对参数 $ w_i $ 的偏导数,有$$ \frac{\partial\text{Obj}}{\partial w_i} = \frac{\partial L}{\partial w_i} + \frac{\gamma\ell_2}{n}w_i. $$
再有参数更新$$ \begin{aligned} w_i\to w'_i &{}\overset{\text{def}}{=} w_i - \eta\frac{\partial L}{\partial w_i} - \eta\frac{\gamma\ell_2}{n}w_i\\ &{}= \biggl(1 - \eta\frac{\gamma\ell_2}{n}\biggr)w_i - \eta\frac{\partial L}{\partial w_i}. \end{aligned} $$
考虑到 $ \eta\frac{\gamma\ell_2}{n} > 0 $,因此,引入 $ L_2 $-正则项之后,相当于衰减了(decay)参数的权重,使参数趋近于零。
$L_1$-正则项与 $L_2$-正则项的区别
现在,我们考虑这样一个问题:为什么使用 $L_1$-正则项,会倾向于使得参数稀疏化;而使用 $L_2$-正则项,会倾向于使得参数稠密地接近于零?
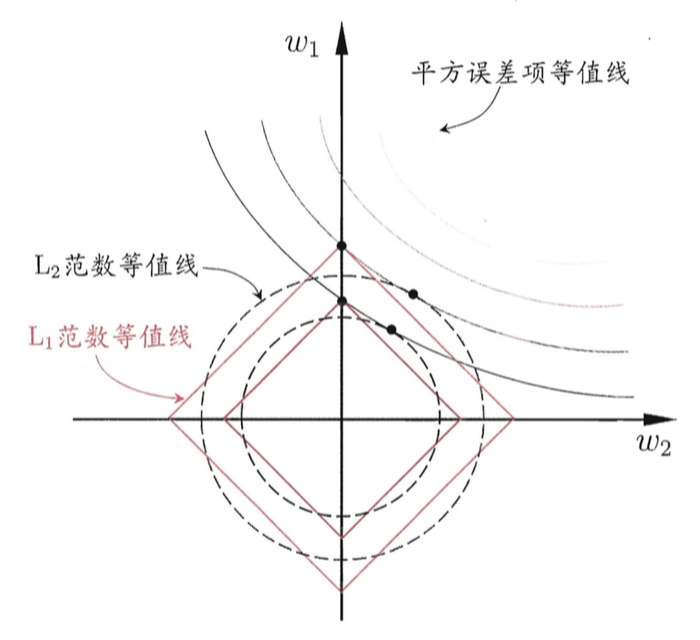
这里引用一张来自周志华老师的著作,《机器学习》(西瓜书)里的插图,尝试解释这个问题。
为了简便起见,我们只考虑模型有两个参数 $w_1$ 与 $w_2$ 的情形。
在图中,我们有三组「等值线」。位于同一条等值线上的 $w_1$ 与 $w_2$,具有相同的值(平方误差、$L_1$-范数或$L_2$-范数)。并且,对于三组等值线来说,当 $(w_1, w_2)$ 沿着等值线法线方向,像外扩张,则对应的值增大;反之,若沿着法线方向向内收缩,则对应的值减小。
因此,对于目标函数 $\text{Obj}(F)$ 来说,实际上是要在正则项的等值线与损失函数的等值线中寻找一个交点,使得二者的和最小。
对于 $L_1$-正则项来说,因为 $L_1$-正则项的等值线是一组菱形,这些交点容易落在坐标轴上。因此,另一个参数的值在这个交点上就是零,从而实现了稀疏化。
对于 $L_2$-正则项来说,因为 $L_2$-正则项的等值线是一组圆形。所以,这些交点可能落在整个平面的任意位置。所以它不能实现「稀疏化」。但是,另一方面,由于 $(w_1, w_2)$ 落在圆上,所以它们的值会比较接近。这就是为什么 $L_2$-正则项可以使得参数在零附近稠密而平滑。
幻灯片
两篇文章对应的幻灯片可在这里下载。