早在学习数学分析时,我就已经接触过卷积的概念。然而,彼时年少,水平有限,没有完整地理解卷积的概念和精髓。这个遗憾一直持续至今。接触到卷积神经网络(Convolution Neural Network, CNN)之后,旧事重提般地,想要了解清楚卷积的冲动就愈发强烈,终至此文。
这是一篇介绍性质的文章。文中的公式、动画效果限于网页的表现力,无法达至完美。本文有对应的 PDF 格式的幻灯片可供下载(离散卷积和卷积神经网络)。你可能需要使用 Adobe Acrobat/Reader 作为 PDF 阅读器,以获得幻灯片的所有效果。
初识卷积
一问卷积
「卷积」这个词给人的第一印象就是「萌萌哒」,因此,恐怕很多人听见卷积的第一反应会是:「卷积可以吃吗为什么要叫这个名字」。
粗暴地回答的话,理由有三:
- 卷在这里对应英文的 convolve 这个单词,在卷积这个概念中,它的本意是「翻转」;
- 积在这里对应乘积,因为卷积是通过两个函数/序列的乘积实现的;
- 它真的是在「卷」——把多个乘积卷在一起变成一个值。
形式定义
在具体介绍卷积是什么、为什么是这样、有什么用之前,让我们预先「先入为主」地看一看一维卷积的定义是什么样的。
- 离散形式:$(x * y)[n] = \sum_{m = -\infty}^{+\infty}x[m]\cdot y[n - m]$。
- 连续形式:$(f * g)(t) = \int_{-\infty}^{+\infty}f(\tau)\cdot g(t - \tau)\mathop{}\!\mathrm{d}\tau$。
当然,此篇主要介绍离散卷积,因此连续卷积从这一刻起就被暂时打入冷宫了。
如果你仔细观察离散卷积的定义,你就会发现,它也可以写成如下等价形式。
$$(x * y)[n] = \sum_{i + k = n}x[i]\cdot y[k].$$
可以看到,卷积将等式右边的两个变量 $i$, $j$ 变成了等式左边的一个变量 $n$——俗称:降维打击。
一维离散卷积
在详细介绍一维离散卷积之前,我们需要先了解什么是「线性时不变系统」。此后,在脉冲激励和冲激响应的叠加中,我们就能得到卷积。
线性时不变系统

线性时不变系统(Linear Time-invariant System)是一种特殊的信号系统。它的特性分成「线性」和「时不变」两个维度。
所谓线性,说的是系统的输出对输入满足齐次性和叠加性。这也就是说,若输入 $x_1(\tau)$ 和 $x_2(\tau)$ 分别得到 $y_1(\tau)$ 和 $y_2(\tau)$,那么对于任意的常数 $c_1$, $c_2$ 满足 $c_1x_1(\tau) + c_2x_2(\tau)$ 的输入在系统的作用下产生输出 $c_1y_1(\tau) + c_2y_2(\tau)$。
| 输入 | 输出 |
|---|---|
$x_1(\tau)$ |
$y_1(\tau)$ |
$x_2(\tau)$ |
$y_2(\tau)$ |
$c_1x_1(\tau) + c_2x_2(\tau)$ |
$c_1y_1(\tau) + c_2y_2(\tau)$ |
所谓时不变,说的是系统对固定输入的输出响应不随时间发生变化。这也就是说,若输入 $x(\tau)$ 得到输出 $y(\tau)$,则若输入 $x(t_0 + \tau)$ 得到输出 $y(t_0 + \tau)$。
| 输入 | 输出 |
|---|---|
$x(\tau)$ |
$y(\tau)$ |
$x(t_0 + \tau)$ |
$y(t_0 + \tau)$ |
冲激和响应
信号系统的输入,称之为「激励」。对信号系统来说,它通常会接收一连串的激励。这一连串的激励,通常在瞬时发生,然后消退。因此信号系统的输入又称之为「脉冲激励」,简称「冲激」。若以 $y$ 记信号系统的冲激,则它应该是一个序列 $y[n]$。具体的值 $y[i]$ 或 $y_i$ 表示第 $i$ 时刻信号系统接收的脉冲激励。
$$y[n] = \{ \ldots, y_{-1} = 0, y_0 = i, y_1 = j, y_2 = k, y_3 = 0, \ldots \}.$$
信号系统的输出,称之为「响应」。对于单位强度冲激的响应,即是「冲激响应」。信号系统对单独的冲激,做出的响应输出,可能在冲激发生之后持续一段时间。若以 $x$ 记信号系统的冲激响应,则它也应该是一个序列 $x[n]$。具体的值 $x[i]$ 或 $x_i$ 表示系统接收到单位强度冲激之后第 $i$ 时刻做出的响应输出。
若你不太理解为何响应会在冲激发生之后持续一段时间,那么你可以把自己比作一个信号系统。当你遇到什么开心/不开心的事情之后,你高兴/伤心的情绪不会只在那一瞬间出现,而是会持续一段时间。
$$x[n] = \{ \ldots, x_{-1} = 0, x_0 = a, x_1 = b, x_2 = c, x_3 = 0, \ldots \}.$$
连续冲激的响应
现在我们知道几个事实:
- 系统接收到一份输入后,其后的一段时间内会陆续给出输出响应;
- 系统会连续收到若干输入;
- 系统是线性时不变的。
特别地,输入冲激 $\hat y$ 在 $x[n]$ 的作用下,第 $i$ 时刻的输出是 $\hat y\cdot x[i]$。因此,整个线性时不变系统在第 $i$ 时刻的输出,应该是
$$y[0]\cdot x[i] + y[1]\cdot x[i - 1] + \cdots.$$
当然,对于两端延伸的无穷序列,你应该把它写作
$$\cdots + y[-1]\cdot x[i + 1] + y[0]\cdot x[i] + y[1]\cdot x[i - 1] + \cdots.$$
以上一小节的数据为例,将数据制成表如下:
| time | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| $y_0 = i$ | $ai$ | $bi$ | $ci$ | $0$ | $0$ |
| $y_1 = j$ | $0$ | $aj$ | $bj$ | $cj$ | $0$ |
| $y_2 = k$ | $0$ | $0$ | $ak$ | $bk$ | $ck$ |
接下来,你只需要纵向观察表格,将每一纵列的值相加,就能得到相应时刻的系统输出响应了。
离散卷积
从上面的分析中,可以看出,对于任意时刻 $n$,系统的输出是
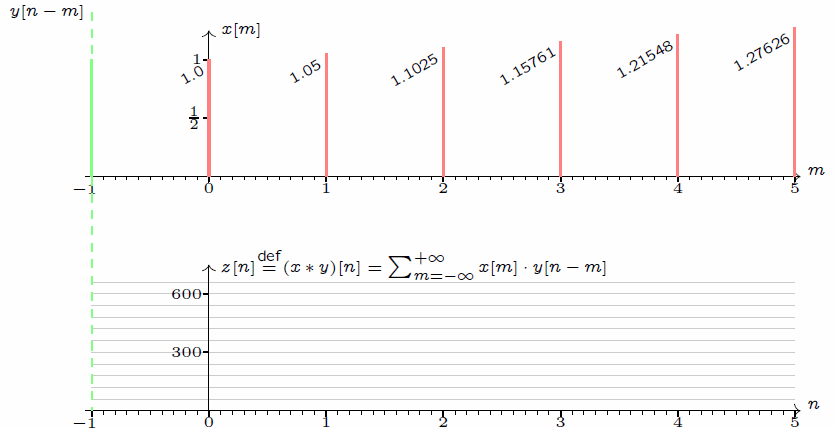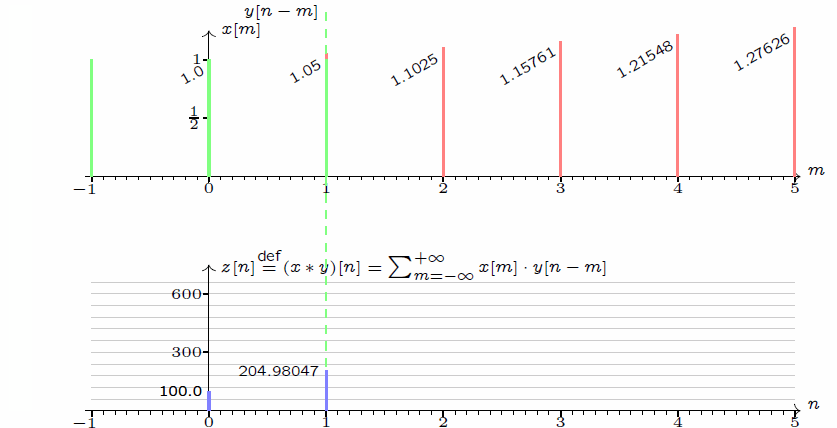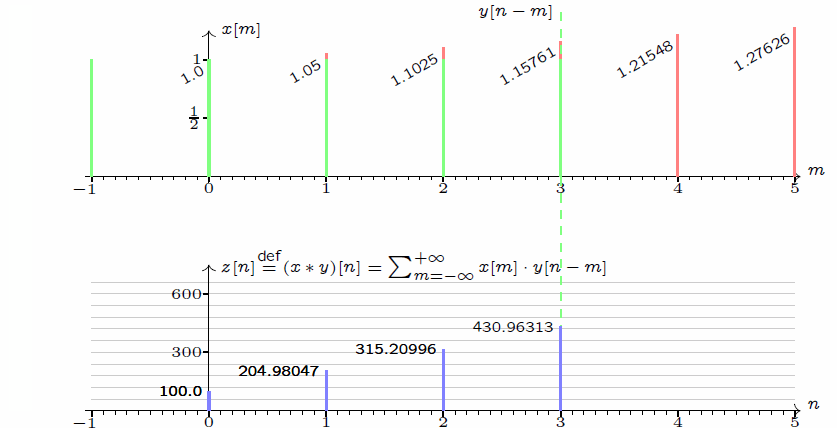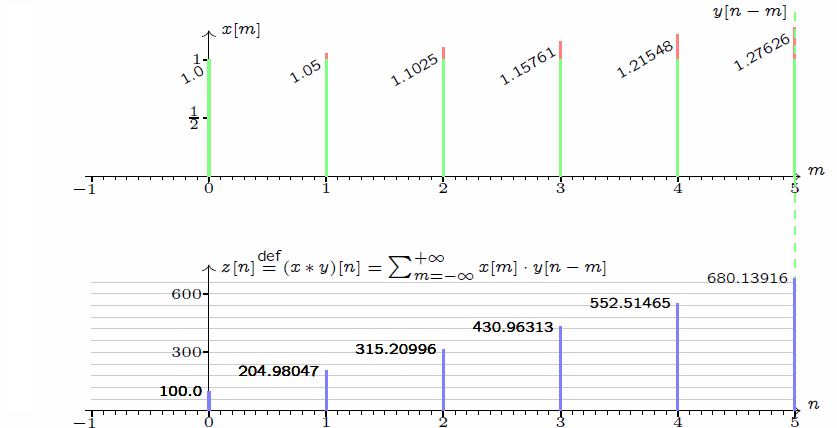
$$z[n] \overset{\text{def}}{=} (x*y)[n] = \sum_{m = -\infty}^{+\infty}x[n - m]\cdot y[m] = \sum_{m = -\infty}^{+\infty}x[m]\cdot y[n - m].$$
这正是一维离散卷积的定义。以 $\sum_{m = -\infty}^{+\infty}x[m]\cdot y[n - m]$ 为例,不难发现,卷积其实是一种推广的加权平均:以 $x$ 为权,以 $n$ 为中心,把 $y$ 距离中心 $-m$ 位置上的值乘上 $x$ 在 $m$ 位置的值,最后加到一起。
定投的例子
现在假设有一个一年期定投项目,它的利率始终保持不变。因此,整个定投项目可以视作是一个线性时不变系统。
- 最终收益对投入的资金是线性累加的;
- 利率不变,意味着任何时候投入资金的效果是一样的。
因此,你可以定义响应序列
$$x[n] = \{ \ldots, x_{-1} = 0, x_0 = 1.05^0, x_1 = 1.05^1, \ldots, x_i = 1.05^i, \ldots \}.$$
而后,假设你每年存入 100 元,于是有冲激序列
$$y[n] = \{ \ldots, y_{-1} = 0, y_0 = 100, y_1 = 100, \ldots, y_i = 100, \ldots \}.$$
于是,任意时刻的账户余额 $z[n] \overset{\text{def}}{=} (x*y)[n]$ 是卷积。
| time | $0$ | $1$ | $2$ | $3$ | $4$ |
|---|---|---|---|---|---|
| $y_0 = 100$ | $100$ | $100\times 1.05^1$ | $100\times 1.05^2$ | $100\times 1.05^3$ | $100\times 1.05^4$ |
| $y_1 = 100$ | $0$ | $100$ | $100\times 1.05^1$ | $100\times 1.05^2$ | $100\times 1.05^3$ |
| $y_2 = 100$ | $0$ | $0$ | $100$ | $100\times 1.05^1$ | $100\times 1.05^2$ |
| $y_3 = 100$ | $0$ | $0$ | $0$ | $100$ | $100\times 1.05^1$ |
| $y_4 = 100$ | $0$ | $0$ | $0$ | $0$ | $100$ |
接下来,我们回过头观察 $\sum_{m = -\infty}^{+\infty}x[m]\cdot y[n - m]$ 这个式子。
若以 $m$ 为「自变量」,则 $y[n - m]$ 相当于把 $y[m]$ 的图像左右翻转(这即是翻转的来源),然后再向右移动 $n$ 个单位。而当 $n$ 增大时,相当于 $x$ 不动而 $y$ 沿着轴线向右滑动。当 $x$ 和 $y$ 重叠时,计算重叠部分的乘积,然后加和得到最终结果。这个加和的过程,放在连续函数的情景下,就是积分了。将这个过程,制作成动态图如下。
怎样卷?
通过观察 $\sum_{m = -\infty}^{+\infty}x[m]\cdot y[n - m]$,我们已经知道了卷积是怎样翻转的,也知道卷积的积分从何而来。现在我们讨论关于卷积的终极问题:究竟要怎样才能「卷起来」?
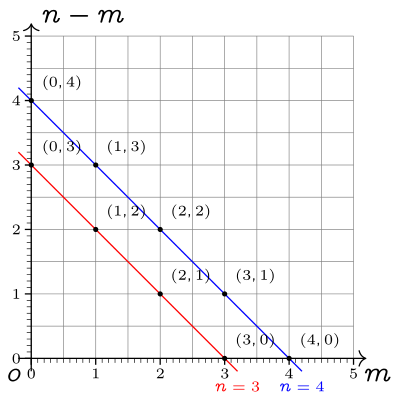
我们来看这张图。它的横轴和纵轴被替换成了 $m$ 和 $n - m$,恰好对应 $\sum_{m = -\infty}^{+\infty}x[m]\cdot y[n - m]$ 中的 $x[m]$ 和 $y[n - m]$。途中有两条斜线,斜线经过的整数交点上画着小黑点。这些小黑点代表相应位置的 $x[m]\cdot y[n - m]$;而斜线则代表将这条斜线上所有小黑点的值相加。
不难发现,$m(n-m)$-二维平面上斜率为 $-1$ 的斜线族,其中每条这样的斜线(包括没有画出来的),都表示了一个卷积。特别地,斜线上每一个整数点的横纵坐标相加(即是 $m + (n - m)$)都是 $n$。因此,斜线对应的卷积是 $(x * y)[n]$。这样,我们就建立了斜线与卷积值之间的对应关系。
现在,把 $m(n-m)$-二维平面想象成一块无限薄的地毯。接下来,我们沿着斜率为 $-1$ 的直线方向,把地毯卷起来。这样,我们就将地毯卷成了一条直线。而这条直线上的每个点,都对应了原平面上的一条直线。也就是说,在「卷地毯」的过程中,原平面的直线纷纷坍缩成了一系列的点。而这些轴线与其上的点,正可作为是卷积 $(x*y)[n]$ 中 $n$ 所在的数轴。
这就是为什么我们说,卷积它真的可以「卷」了。
二问卷积
至此,一维离散卷积相关的内容,我们就介绍完了。现在我们回过头来看看,在介绍一维离散卷积的过程中,卷积表现出了哪些特点。
我们是通过线性时不变的信号系统引出卷积的概念的。若仍以信号系统的说辞为例,则不难发现:
- 一个脉冲激励可以影响到信号系统在若干时刻的输出;
- 从另一个角度,这也就是说,信号系统任意时刻的输出,取决于相关的多个冲激输入。
也就是说,和一般的函数不同,信号系统的输入和输出不是「一对一」的关系,而是「多对多」的关系。我们在后续介绍卷积神经网络的时候,会看到这一特点的作用。
此外,仍以信号系统的说辞为例,我们也不难发现,系统的最终输出,一方面取决于输入的激励信号长什么样子,另一方面取决于冲激响应的模式。这两方面相互作用(就是卷积),最终决定了信号系统的输出。
在后续对一维离散卷积的观察中,我们发现,连续地求解多个卷积值的时候(即,求解 $n = 0, 1, 2, \ldots$ 的卷积值时),我们实际上做的事情可以归纳成:
- 翻转输入信号;
- 输入信号沿轴线向前滑动;
- 输入信号与冲激响应叠加的部分分别求积,然后相加。
而实际上我们发现,在卷积的定义中,$x$ 和 $y$ 是地位等同的。这就是说,我们也完全可以选择翻转而后滑动冲激响应的模式,再去求积、叠加。此时,我们通常会把冲激响应称为「卷积核」,而把整个过程形象地称之为:滑动卷积核。
二维离散卷积
定义
恭喜你,现在我们进入「高维宇宙」。
首先,让我们回顾一下一维离散卷积的定义。
$$(x*y)[n] \overset{\text{def}}{=} \sum_{m = -\infty}^{+\infty}x[m]\cdot y[n - m].$$
二维卷积的定义,在形式上和一维卷积完全一致——只需要将一维卷积中的变量 $m$, $n$ 从标量变成向量即可。当然,你也可以将向量的两个分量展开,记成标量形式。
$$ \begin{aligned} (x*y)[\vec n] \overset{\text{def}}{=}{}& \sum_{\vec m = (-\infty, -\infty)}^{(+\infty, +\infty)}x[\vec m]\cdot y[\vec n - \vec m] \\ (x*y)[n_1, n_2] \overset{\text{def}}{=}{}& \sum_{m_1 = -\infty}^{+\infty}\sum_{m_2 = -\infty}^{+\infty}x[m_1, m_2]\cdot y[n_1 - m_1, n_2 - m_2]. \end{aligned} $$
类似地,你可以定义更高维的卷积。
若仔细观察公式,不难发现,我们在二维卷积中遇到的问题,和在一维卷积中遇到的问题完全一致。二维卷积具有和一维卷积几乎完全相同的性质、特点、作用。和一维卷积一样,二维卷积也可以看做是加权平均的推广:以 $x$ 为权,以 $(n_1, n_2)$ 位中心,将 $y$ 距离中心 $(-m_1, -m_2)$ 位置的值乘上 $x$ 距离中心 $(m_1, m_2)$ 的值,最后加到一起。
图像的滤镜
在实际应用中,卷积核 $x$ 的有效部分总是有限的。例如,下图展示了一个 $3\times 3$ 的卷积核,在图像上的滑动。
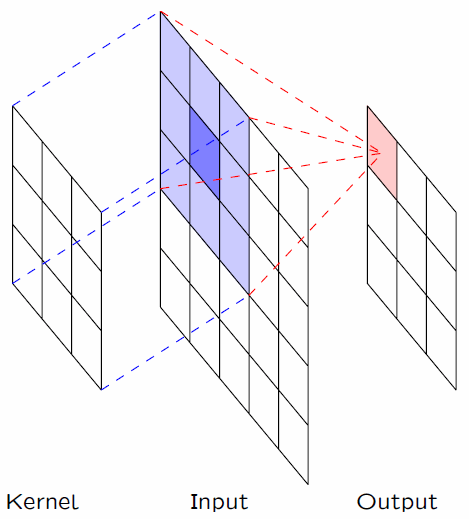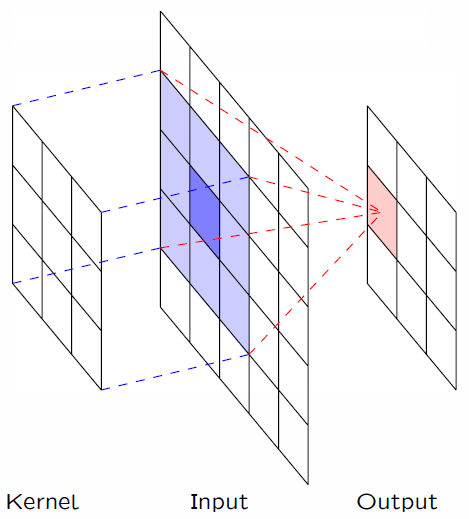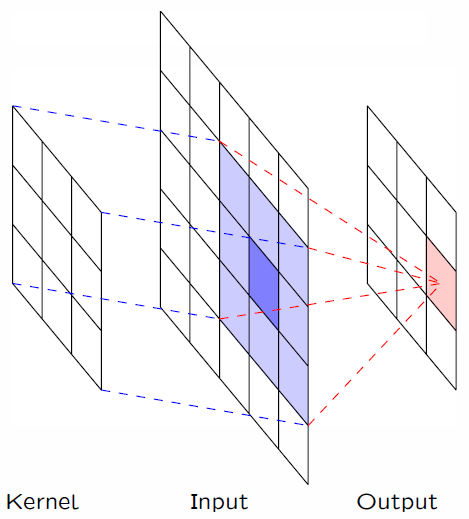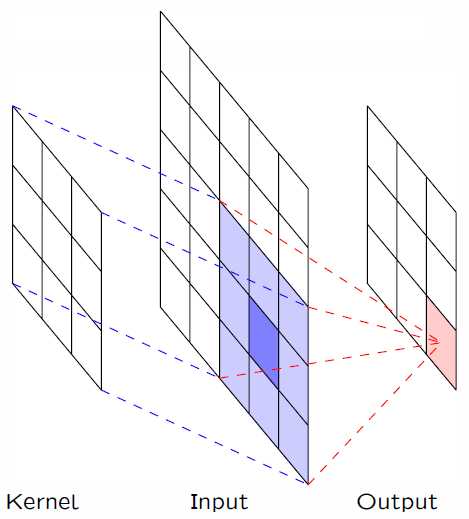
值得一提的是,对于图像来说,这个过程实际就是 PhotoShop 等图像处理软件中的「滤镜」效果。比如,假设我们有一个 $3\times 3$ 的卷积核
$$ \begin{bmatrix} 1/9 & 1/9 & 1/9 \\ 1/9 & 1/9 & 1/9 \\ 1/9 & 1/9 & 1/9 \end{bmatrix}, $$
从直觉上分析,它将中心点附近的共 9 个点的像素值,平均到输出图像的中心像素点上;这实际上就是模糊效果对应的滤镜(box-blur)。又比如,假设我们有这样的卷积核
$$ \begin{bmatrix} 0 & -1 & 0 \\ -1 & 5 & -1 \\ 0 & -1 & 0 \\ \end{bmatrix}, $$
从直觉上分析,它加强了中心像素点的作用,同时减小了位于其上下左右的四个像素点对它的干扰;这实际上就是锐化效果对应的滤镜(sharpen)。又比如,假设我们有这样的卷积核
$$ \begin{bmatrix} -1 & -1 & -1 \\ -1 & 8 & -1 \\ -1 & -1 & -1 \\ \end{bmatrix}, $$
从直觉上分析,只有当中心像素点原本的像素值和周围 8 个像素点的值差距很大时,这个卷积核的输出,才会明显地不等于 0;因此,这实际上就是边缘检测对应的滤镜(edge detect)。
我们将上述三个矩阵以 Python 实现出来,就能看到它们的效果了。(参见:PIL 简明教程 - 像素操作与图像滤镜)其效果如下图所示。

三问卷积
又到了思考问题的贤者时间。
在介绍一维卷积的过程中,我们已经讨论了卷积本身具有的特点。但是,也留下了一个问题:卷积在抽象上,到底有什么意义呢?
站在人类的角度,我们先入为主地将上面 3 个示例的卷积核当做了「滤镜」。然而,事情真的是这样吗?如果我们忘记「滤镜」这一先验知识,那么我们可能会把这件事情,简单地以更抽象的方式描述为「卷积核处理图形」。没错,这仅仅是一个「处理」过程而已。现在我们回想一下,环境中的真实景象,也是经过我们的大脑处理之后,在脑海里形成实际的画面的。若然你知道,同一个真实景象,在不同生物的眼里是不一样的。那么你就不难发现,不同的生物,因其进化路径不同,大脑对环境真实景象的处理也不同,因而脑海中看到的景象也就不同。这与我们用不同的滤镜处理图像,得到不同的滤镜结果,何其相似?
刚才我们说到不同生物眼里的世界是不一样的。那么,更深入地理解一下这份不同,我们会否领会到更多的东西呢?
比如,我们可以思考:为什么自然选择会让不同的生物看到不同的景象?答案其实很简单:因为适者生存。蛇类的眼睛,按照人类的意识,几乎不能视物;然而因为经常需要夜间活动,所以蛇能够以红外的方式「看到」这个世界。青蛙的眼睛,难以察觉到静止的事物;然而因为它只对「会动的虫子」感兴趣,所以青蛙具有奇佳的动态视觉。站在更广的时间维度上,我们可以这样回答这个问题:对于具体的某种生物来说,因其生存需要,它只对某种形式的视觉效果感兴趣,因而其视觉处理系统进化成了当前的模样。简而言之,不同的生物,看待世界的方式,有不同的侧重点,因而将同一个真实景象处理成了不同的模样。
这里我们对生物的视觉效果进行了展开分析。这不是我要「跨界」当「神棍」,而是想以一种直觉的方式,以普遍的现象为对比,试着能够更好地理解卷积的意义。
至此,我们可以比较容易地制作出一张对应的表格。
| 卷积 | 生物视觉 | 机器学习领域的意义 |
|---|---|---|
| 滑动卷积核 | 视觉系统处理外界光信号 | 读入并处理结构化的特征 |
| 卷积核处理的结果 | 脑海中形成的视觉成像 | 卷积处理的结果 |
| 不同的卷积核 | 观察世界的不同方式、不同侧重点 | 不同角度的高维特征信号 |
这也就是说,特定的卷积核,能够从若干相关特征信号(通常是相邻位置的特征信号)中以特定的方式抽取新的高维特征。
卷积神经网络
有了这些关于卷积的知识基础,现在我们可以讨论卷积神经网络了。我们假设你已经对神经网络有所了解,因此就不去从感知机开始,逐步地介绍了。
图片识别任务
这个例子,来自于 YJango的卷积神经网络——介绍。
在介绍二维离散卷积的时候,我们以图片为例。这是因为,图片是天然的二维像素矩阵组成的数据形式(RBG 三通道即是 3 个矩阵)。因此,专业里我们也以图片识别任务为例,展开对卷积神经网络的介绍。
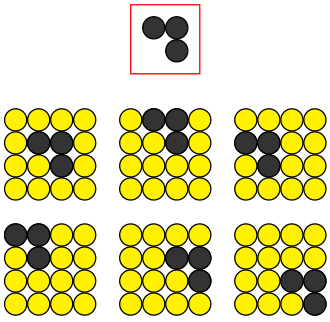
如上图。每一个 $4 \times 4$ 的方块,都表示一张图片。在我们的表示中,黄色的圆圈表示空无一物的底色;黑色的圆圈,表示有内容的笔画。现在,我们要识别上图顶部的「横折」这一笔画。显而易见,上图下半部分的 6 张图片,内里都包含了横折。
前馈神经网络
对于这样的图片识别任务,使用深度前馈神经网络来解决,当然是可以的。
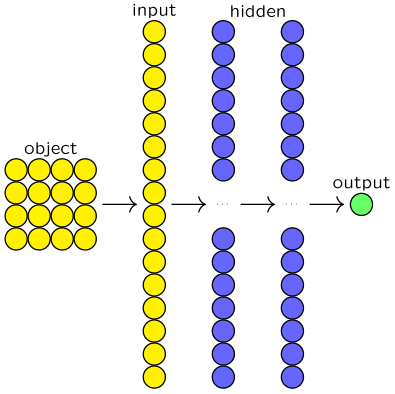
如上图。为了解决这样的问题,我们首先需要将原始图片制成一个能用向量表示出来的数据形式。最简单的办法,就是将二维的图像,逐行地展开。如此,我们就从 object 得到了输入层 input。接下来,我们就可以把输入层链接到隐藏层当中,经过逐层地全连接,得到最终输出 output。通常来说,这个最终输出,是神经网络给出的概率。这个概率描述,神经网络认为当前图片中,包含「横折」的概率。
经过大量的训练,这样的神经网络可以很好地完成识别任务。然而,这样的网络设计,也可能存在一些问题。

如上图。假设左侧的 4 张图片,是我们标注好的训练样本。经过训练之后,我们的神经网络应当已经具有一定的能力,尝试识别图片中是否存在「横折」这一笔画。然而,由于训练神经网络时的输入样本十分有限,我们的神经网络可能并不认得右侧的样本。特别地,在我们的神经网络示意图中,左上角的横折和位于中间的横折是完全不同的两个向量。因此,我们得到的神经网络模型,很可能无法给出对右侧未知样本的准确预测。
那么,怎么办呢?
最最简单容易想到的办法,就是增加训练时的训练样本。若然我们能够让样本覆盖所有情况,那么训练得到的神经网络自然就可以识别所有的情况,并给出结论了。不过,最简单容易想到的解法,往往暗含各种各样的问题。首先,我们的图片识别任务中,图片都是 $4 \times 4$ 的小型图片。对这类图片,穷举所有可能,其总数也只有 $2^{16}$ 张。对于这种类型的问题,穷举所有情况,大致是没有问题的。然而,实际生产中,我们遇到的问题,其复杂度要远远高于现在我们所言的「玩具问题」。在实际问题中,我们不可能让样本覆盖所有情形。另一方面,若是简单粗暴地扩增样本容量,就失去了模型「预测」的意义了。换而言之,这就不是我们追求的高可泛化的模型了。
表意的平移不变性——对问题的深入思考
扩大训练集的解法,当然也是一个办法。在实际生产中,有些时候也确实需要扩大训练集,以解决一些欠拟合的问题。然而,正如任何定理都有其适用范围,我们也需要斟酌扩大训练集在当前任务中是否合适。显然,有上面的分析,在当前任务中,这不是个好办法。
那么,问题出在哪里呢?或者说,我们应当在哪个方向前进,以便解决这个问题呢?在上面的分析中,我们有提到一句话:「在我们的神经网络示意图中,左上角的横折和位于中间的横折是完全不同的两个向量」。我想,若你足够敏感,应该能意识到什么。
不好。这很不好。在表意上,位于图片左上角的横折之于位于图片中间的横折没有什么差别。也就是说,在图片上任意平移横折的位置,其表意不发生变化。我们称之为表意的平移不变性。然而,在我们的神经网络中,这两个横折在输入层的表现居然没有什么共同点。显而易见,这是不合理的。因此,在遇到的这个问题中,我们首先应该考虑的,不是扩增训练集,而是应当考虑我们神经网络是否足够好地适应当前的问题。
那么,我们的神经网络中,问题出在哪里呢?
首先,我们的神经网络是针对每个像素的具体情况进行训练的。其次,图片上的区域各自为政,没有关联。也就是说,我们的神经网络,很难捕捉到相邻区域中几个像素点(特征值)的结构信息。另一方面,我们的神经网络,也没有以一种一致地视角,去看待每一个局部的结构。这样一来,我们的神经网络就可能会把位于左上角的横折与位于中间的横折,当成两个完全没有关联的图形。这显然是不合适的。
引入卷积
至此,就轮到卷积出场拯救世界了。
我们回顾一下简单的前馈神经网络在当前任务中遇到的问题:无法一致地捕捉局部的结构信息。我们再来回想一下卷积的特点:以一个固定的卷积核,收集相邻特征信号的信息,加权平均得到卷积值。啊!卷积的这些特点,不就正好弥补了当前前馈神经网络的不足吗?
于是,我们可以设计出这样的网络结构。
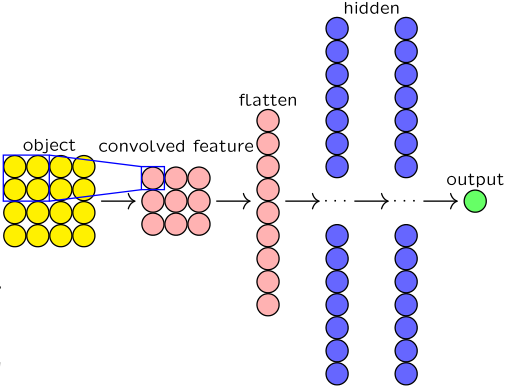
如上图。首先,我们用一个固定的 $2 \times 2$ 的卷积核作为窗口,逐个像素地扫描原图片。这样一来,我们可以得到 $3 \times 3$ 的卷积结果,称为 convolved feature。而后,和我们在前馈神经网络中做的一样,我们将 convolved feature 展开,作为输入层,链接其背后的隐藏层,并最终得到输出。
在这个过程中,神经网络的参数,除了隐藏层中的各个神经元上的参数,还有卷积核的具体内容。也就是说,卷积核的大小是固定的,但是它长什么样子,是需要具体训练的。
这样引入了卷积的神经网络,就是卷积神经网络(Convolution Neural Network, CNN)了。当然,在实际使用中,还常常引入名为池化(Pooling)的技术,这里按下不表。
不变性的讨论
有了卷积,我们的神经网络就能一致地去捕捉输入信号局部的结构信息。特别地,由于卷积核在不同位置上是共享的,所以笔画的平移在神经网络看来,就不影响表意了。因此我们说,卷积神经网络满足了平移不变性。
那么,是否还有其它的不变性呢?当然是有的。
比如,我们现在的横折由 $3$ 个像素在 $2 \times 2$ 的局部中组成。那么,若是将它放大,在 $3 \times 3$ 的局部中,用 $5$ 个像素去组成横折,是否也可以呢?答案是显而易见的:大猫也是猫,大狗也是狗。这种现象,我们称之为缩放不变性。那么,当前的卷积神经网络,是否能解决这样的问题呢?我们说,不能。因为我们当前使用的卷积核是 $2 \times 2$ 的,它无法去捕捉 $3 \times 3$ 的局部结构中的完整信息。因此,当前的卷积神经网络,没有满足缩放不变性。若要满足缩放不变性,我们可以考虑用不同大小的卷积核,分别处理原图像;或者,可以考虑在卷积层的基础上,再用卷积处理一次。
又比如,假设我们不识别笔画,我们识别图片中的铅笔。在图片中,除了说铅笔可大可小,位置上可以在图片上游走,铅笔还可能以不同角度出现——横着放的、竖着放的、斜着放的。但不论铅笔如何摆放,它都是铅笔。这种现象,我们称之为旋转不变性。不过,很遗憾,由于卷积的特性所限,我们无法简单地用卷积,让神经网络满足旋转不变性。
卷积神经网络直觉上的优势
上面我们讨论了卷积的特点。因此,我们不难总结卷积神经网络的一些优势。
- 适用于相关元素(特别是相邻元素)中存在结构特征的情况;
- 适用于上述结构可能出现在不同位置的情况。
现在,我们考虑一下分类问题。对于分类问题来说
- 在分割线(可能是超平面、超曲面)附近,样本往往存在特定的结构特征;
- 输入的样本,可能位于分割线的不同位置,因此上述结构也可能出现在分割线的不同位置。
分类问题的这样的特点,恰恰符合了卷积神经网络的优势。因此,人们常常偏向于认为:「卷积神经网络可以在分类问题上表现得好」。


