看似高大上的人工智能、机器学习,实际上都脱不开数学的支持。在这些数学内容中,最重要的无疑是两个部分:代数和概率论。我无法在博客中完整地介绍代数(特别是矩阵论)和概率论,但是将其中部分有趣又重要的内容提出来讲解,还是可行的。
此篇,我们谈谈矩阵的 SVD 分解。
一些矩阵知识
首先我们来看一些基本的矩阵知识。
转置与共轭转置
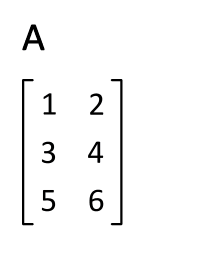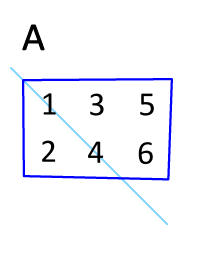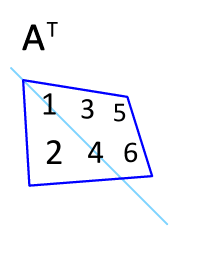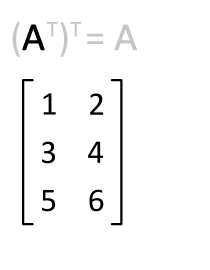
矩阵的转置(transpose)是最简单的一种矩阵变换。简单来说,若 $m\times n$ 的矩阵 $\mathbf M$ 的转置记为 $\mathbf M^{\mathsf T}$;则 $\mathbf M^{\mathsf T}$ 是一个 $n\times m$ 的矩阵,并且 $\mathbf M_{i,j} = \mathbf M^{\mathsf T}_{j,i}$。
因此,矩阵的转置相当于将矩阵按照主对角线翻转;同时,我们不难得出 $\mathbf M = \bigl(\mathbf M^{\mathsf T}\bigr)^{\mathsf T}$。
矩阵的共轭转置(conjugate transpose)可能是倒数第二简单的矩阵变换。共轭转置只需要在转置的基础上,再叠加复数的共轭即可。因此,若以 $\mathbf M^{\mathsf H}$ 记矩阵 $\mathbf M$ 的共轭转置,则有 $\mathbf M_{i,j} = \overline{\bigl(\mathbf M^{\mathsf H}\bigr)_{j,i}}$。
酉矩阵
酉矩阵(unitary matrix)是一种特殊的方阵,它满足
$$ \mathbf U\mathbf U^{\mathsf H} = \mathbf U^{\mathsf H}\mathbf U = I_n.$$
不难看出,酉矩阵实际上是推广的正交矩阵(orthogonal matrix);当酉矩阵中的元素均为实数时,酉矩阵实际就是正交矩阵。另一方面,由于 $\mathbf M\mathbf M^{-1} = \mathbf M^{-1}\mathbf M = I_n$,所以酉矩阵 $\mathbf U$ 满足 $\mathbf U^{-1} = \mathbf U^{\mathsf H}$;事实上,这是一个矩阵是酉矩阵的充分必要条件。
正规矩阵
同酉矩阵一样,正规矩阵(normal matrix)也是一种特殊的方阵,它要求在矩阵乘法的意义下与它的共轭转置矩阵满足交换律。这也就是说,若矩阵 $\mathbf M$ 满足如下条件,则称其为正规矩阵:
$$\mathbf M\mathbf M^{\mathsf H} = \mathbf M^{\mathsf H}\mathbf M.$$
显而易见,复系数的酉矩阵和实系数的正交矩阵都是正规矩阵。显而易见,正规矩阵并不只有酉矩阵或正交矩阵。例如说,矩阵 $\mathbf M = \begin{pmatrix}1 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1\end{pmatrix}$ 即是一个正规矩阵,但它显然不是酉矩阵或正交矩阵;因为
$$\mathbf M\mathbf M^{\mathsf H} = \begin{pmatrix}2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2\end{pmatrix} = \mathbf M^{\mathsf H}\mathbf M.$$
谱定理和谱分解
矩阵的对角化是线性代数中的一个重要命题。谱定理(spectral theorem)给出了方阵对角化的一个结论:若矩阵 $\mathbf M$ 是一个正规矩阵,则存在酉矩阵 $\mathbf U$,以及对角矩阵 $\mathbf \Lambda$,使得
$$\mathbf M = \mathbf U\mathbf \Lambda\mathbf U^{\mathsf H}.$$
这也就是说,正规矩阵,可经由酉变换,分解为对角矩阵;这种矩阵分解的方式,称为谱分解(spectral decomposition)。
SVD 分解
谱定理给出了正规矩阵分解的可能性以及分解形式。然而,对于矩阵来说,正规矩阵是要求非常高的。因此,谱定理是一个非常弱的定理,它的适用范围有限。在实际生产中,我们遇到的很多矩阵都不是正规矩阵。对于这些矩阵,谱定理就失效了。作为谱定理的泛化,SVD 分解对于原矩阵的要求就要弱得多。
SVD 分解说的是:假设 $\mathbf M$ 是一个 $ m\times n$ 的矩阵,其中的元素全部属于数域 $\mathbb K$(实数域 $\mathbb R$ 或复数域 $\mathbb C$)。那么,存在 $m\times m$ 的酉矩阵 $\mathbf U$ 和 $n\times n$ 的酉矩阵 $\mathbf V$ 使得
$$\mathbf M = \mathbf U\mathbf\Sigma\mathbf V^{\mathsf H},$$
其中 $\mathbf\Sigma$ 是 $m\times n$ 的非负实数对角矩阵;并且 $\mathbf\Sigma$ 对角线上的元素 $\mathbf\Sigma_{i, i}$ 是 $\mathbf M$ 的奇异值。一般来说,我们偏好将这些奇异值按从大到小的顺序排列,这样一来 $\mathbf\Sigma$ 就由 $\mathbf M$ 唯一确定了。
另一方面,因为 $\mathbf U$ 和 $\mathbf V$ 都是酉矩阵,所以 $\mathbf U$ 和 $\mathbf V$ 的列向量分别张成 $\mathbb K^{m}$ 和 $\mathbb K^{n}$ 的一组标准正交基。我们将 $\mathbf U$ 的列向量记作 $\vec u_i,; 1 \leqslant i\leqslant m$;将 $\mathbf V$ 的列向量记作 $\vec v_j,; 1\leqslant j\leqslant n$;同时,将 $\mathbf\Sigma$ 对角线上的第 $i$ 个元素记作 $\sigma_k,; 1\leqslant k\leqslant\min(m,n)$。那么,SVD 分解实际可以将矩阵 $\mathbf M$ 写作一个求和形式
$$\mathbf M = \sum_{i = 1}^{\min(m, n)}\sigma_i\vec u_i\vec v_i^{\mathsf T}.$$
SVD 的计算方法
了解了 SVD 的介绍和相关几何解释之后,接下来最直接想要知道的就是如何计算一个矩阵的 SVD 了。我们分成几步来探讨这个问题。
SVD 与特征值
现在,假设矩阵 $\mathbf M_{m\times n}$ 的 SVD 分解是
$$\mathbf M = \mathbf U\mathbf\Sigma\mathbf V^{\mathsf H};$$
那么,我们有
$$\begin{aligned} \mathbf M\mathbf M^{\mathsf H} &{}= \mathbf U\mathbf\Sigma\mathbf V^{\mathsf H}\mathbf V\mathbf\Sigma^{\mathsf H}\mathbf U^{\mathsf H} = \mathbf U(\mathbf\Sigma\mathbf\Sigma^{\mathsf H})\mathbf U^{\mathsf H}\\ \mathbf M^{\mathsf H}\mathbf M &{}= \mathbf V\mathbf\Sigma^{\mathsf H}\mathbf U^{\mathsf H}\mathbf U\mathbf\Sigma\mathbf V^{\mathsf H} = \mathbf V(\mathbf\Sigma^{\mathsf H}\mathbf\Sigma)\mathbf V^{\mathsf H}\\ \end{aligned}$$
这也就是说,$\mathbf U$ 的列向量(左奇异向量),是 $\mathbf M\mathbf M^{\mathsf H}$ 的特征向量;同时,$\mathbf V$ 的列向量(右奇异向量),是 $\mathbf M^{\mathsf H}\mathbf M$ 的特征向量;另一方面,$\mathbf M$ 的奇异值($\mathbf\Sigma$ 的非零对角元素)则是 $\mathbf M\mathbf M^{\mathsf H}$ 或者 $\mathbf M^{\mathsf H}\mathbf M$ 的非零特征值的平方根。
如何计算 SVD
有了这些知识,我们就能手工计算出任意矩阵的 SVD 分解了;具体来说,算法如下
- 计算 $\mathbf M\mathbf M^{\mathsf H}$ 和 $\mathbf M^{\mathsf H}\mathbf M$;
- 分别计算 $\mathbf M\mathbf M^{\mathsf H}$ 和 $\mathbf M^{\mathsf H}\mathbf M$ 的特征向量及其特征值;
- $\mathbf M\mathbf M^{\mathsf H}$ 的特征向量组成 $\mathbf U$;而 $\mathbf M^{\mathsf H}\mathbf M$ 的特征向量组成 $\mathbf V$;
- 对 $\mathbf M\mathbf M^{\mathsf H}$ 和 $\mathbf M^{\mathsf H}\mathbf M$ 的非零特征值求平方根,对应上述特征向量的位置,填入 $\mathbf\Sigma$ 的对角元。
实际计算看看
现在,我们来试着计算 $\mathbf M = \begin{bmatrix}2 & 4 \\ 1 & 3 \\ 0 & 0 \\ 0 & 0\end{bmatrix}$ 的奇异值分解。计算奇异值分解,需要计算 $\mathbf M$ 与其共轭转置的左右积;这里主要以 $\mathbf M\mathbf M^{\mathsf H}$ 为例。
首先,我们需要计算 $\mathbf M\mathbf M^{\mathsf H}$,
$$ \mathbf W = \mathbf M\mathbf M^{\mathsf H} = \begin{bmatrix}2 & 4 \\ 1 & 3 \\ 0 & 0 \\ 0 & 0\end{bmatrix}\begin{bmatrix}2 & 1 & 0 & 0 \\ 4 & 3 & 0 & 0\end{bmatrix} = \begin{bmatrix}20 & 14 & 0 & 0 \\ 14 & 10 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0\end{bmatrix}. $$
现在,我们要求 $\mathbf W$ 的特征值与特征向量。根据定义 $\mathbf W\vec x = \lambda \vec x$;因此 $(\mathbf W - \lambda\mathbf I)\vec x = \vec 0$。这也就是说
$$ \begin{bmatrix} 20 - \lambda & 14 & 0 & 0 \\ 14 & 10 - \lambda & 0 & 0 \\ 0 & 0 & -\lambda & 0 \\ 0 & 0 & 0 & -\lambda \end{bmatrix}\vec x = \vec 0. $$
根据线性方程组的理论,若要该关于 $\vec x$ 的方程有非零解,则要求系数矩阵的行列式为 0;也就是
$$ \begin{vmatrix} 20 - \lambda & 14 & 0 & 0 \\ 14 & 10 - \lambda & 0 & 0 \\ 0 & 0 & -\lambda & 0 \\ 0 & 0 & 0 & -\lambda \end{vmatrix} = \begin{vmatrix} 20 - \lambda & 14 \\ 14 & 10 - \lambda \\ \end{vmatrix}\begin{vmatrix} -\lambda & 0 \\ 0 & -\lambda \\ \end{vmatrix} = 0, $$
这也就是 $\bigl((20 - \lambda)(10 - \lambda) - 196\bigr)\lambda^2 = 0$;解得 $\lambda_{1} = \lambda_{2} = 0$, $\lambda_{3} = 15 + \sqrt{221} \approx 29.866$, $\lambda_{4} = 15 - \sqrt{221} \approx 0.134$。将特征值代入原方程,可解得对应的特征向量;这些特征向量即作为列向量,形成矩阵
$$\mathbf U = \begin{bmatrix}-0.82 & -0.58 & 0 & 0 \\ -0.58 & 0.82 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{bmatrix}.$$
同理可解得(注意,$\mathbf M\mathbf M^{\mathsf T}$ 和 $\mathbf M^{\mathsf T}\mathbf M$ 的特征值相同)
$$\mathbf V = \begin{bmatrix}-0.40 & -0.91 \\ -0.91 & 0.40\end{bmatrix}.$$
以及 $\mathbf\Sigma$ 上的对角线元素由 $\mathbf W$ 的特征值的算术平方根组成;因此有
$$\mathbf\Sigma = \begin{bmatrix}5.46 & 0 \\ 0 & 0.37 \\ 0 & 0 \\ 0 & 0\end{bmatrix}.$$
因此我们得到矩阵 $\mathbf M$ 的 SVD 分解(数值上做了近似):
$$\begin{bmatrix}2 & 4 \\ 1 & 3 \\ 0 & 0 \\ 0 & 0\end{bmatrix} \approx \begin{bmatrix}-0.82 & -0.58 & 0 & 0 \\ -0.58 & 0.82 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{bmatrix}\begin{bmatrix}5.46 & 0 \\ 0 & 0.37 \\ 0 & 0 \\ 0 & 0\end{bmatrix}\begin{bmatrix}-0.40 & -0.91 \\ -0.91 & 0.40\end{bmatrix}$$
几何上的直观解释
我们先来看一个例子。假设 $\mathbf M$ 是一个 $m\times n$ 的矩阵,而 $\mathbf x$ 是线性空间 $\mathbb K^n$ 中的向量,则
$$\mathbf y = \mathbf M\cdot\mathbf x$$
是线性空间 $\mathbb K^m$ 中的向量。这样一来,矩阵 $\mathbb A$ 就对应了一个从 $\mathbb K^n$ 到 $\mathbb K^m$ 的变换 $T: \mathbb K^n \to \mathbb K^m$,具体来说既是 $\mathbf x\mapsto \mathbf M\cdot\mathbf x$。
这也就是说,在线性代数中,任意矩阵都能看做是一种变换。这样一来,我们就统一了矩阵和变换。
旋转变换和反射变换(镜像)
在线性空间中进行旋转,实际是要改变向量的方向,但是不改变向量的长度和手性。现在假设矩阵 $\mathbf M_{n\times n}$ 是线性空间 $\mathbf R^{n}$ 中的一个旋转变换对应的矩阵,我们来看看它应该是什么样子。
首先,我们考虑向量内积 $\vec a\cdot\vec b = \lvert\vec a\rvert\lvert\vec b\rvert\cos\langle\vec a,\vec b\rangle$。因为旋转不改变向量的长度,且两个向量经过相同的旋转之后,其夹角保持不变。因此,若 $\mathbf M$ 对应一个旋转变换,那么就必须有
$$\vec a\cdot\vec b = \mathbf M\vec a\cdot \mathbf M\vec b,$$
也就是
$$\vec a\cdot\vec b^{\mathsf T} = \mathbf M\vec a\cdot (\mathbf M\vec b)^{\mathsf T},$$
这也就是说 $\mathbf M\mathbf M^{\mathsf T} = \mathbf I_{n}$,亦即 $\mathbf M$ 是正交矩阵。
因此,对于二维的情况,$\mathbf M$ 可以写作 $\begin{bmatrix}\cos\varphi & -\sin\varphi \\ \sin\varphi & \cos\varphi\end{bmatrix}$ 或 $\begin{bmatrix}\cos\varphi & \sin\varphi \\ \sin\varphi & -\cos\varphi\end{bmatrix}$。前者行列式为 $1$ 而后者行列式为 $-1$。既然 $\mathbf M$ 是正交矩阵,那么它的行列式值必然是 $\pm 1$。现在的问题是,行列式为 $1$ 和 $-1$ 究竟哪一个才是旋转?或者两个都是旋转?
回过头,我们需要注意两件事情。其一,在旋转的定义中,我们提出了旋转保持「手性」;其二,在得出旋转矩阵是正交矩阵的过程中,我们并没有运用到「手性不变」这一特性——因为 $\cos\langle\vec a,\vec b\rangle = \cos\langle\vec b,\vec a\rangle$。
事实上,若 $\mathbf M$ 的行列式为 $-1$,则该矩阵对应了一个瑕旋转——先旋转 $\varphi$ 而后按直线 $r = k\varphi$ 镜像。考虑 $\varphi - \alpha = 2\varphi - (\varphi + \alpha)$,这一瑕旋转实质上就是按直线 $r = k(\varphi / 2)$ 镜像。
因此我们说,旋转矩阵是一个行列式为 $1$ 的正定矩阵,其形式为
$$\begin{bmatrix}\cos\varphi & -\sin\varphi \\ \sin\varphi & \cos\varphi\end{bmatrix},$$
表示向正方向(通常是逆时针方向)旋转 $\varphi$。对于 $\mathbb R^{2}$ 上的标准正交基 $\begin{bmatrix}1 \\ 0\end{bmatrix}$, $\begin{bmatrix}0 \\ 1\end{bmatrix}$,他们分别被变换为 $\begin{bmatrix}\cos\varphi \\ \sin\varphi\end{bmatrix}$ 和 $\begin{bmatrix}-\sin\varphi \\ \cos\varphi\end{bmatrix}$。
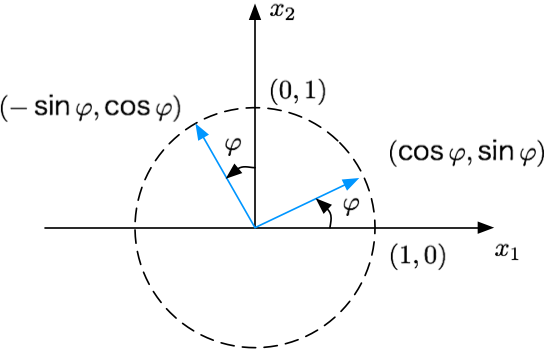
行列式为 $-1$ 的正定矩阵,其形式为
$$\begin{bmatrix}\cos\varphi & \sin\varphi \\ \sin\varphi & -\cos\varphi\end{bmatrix},$$
表示按直线 $r = k(\varphi / 2)$ 镜像。
缩放变换
在线性空间中进行缩放,实质就是要让线性空间中的每一维独立地进行变换,而不受其他维度影响。这样一来,很显然,对应的矩阵应该是对角矩阵。
SVD 分解的几何解释
现在回过头来看 SVD 分解
$$\mathbf M = \mathbf U\mathbf\Sigma\mathbf V^{\mathsf H},$$
在实数范围内讨论,我们实质上是将一个复杂的变换 $M:\mathbb R^{m}\to\mathbb R^{n}$ 分解成了三个变换:旋转/镜像 $U:\mathbb R^{m}\to\mathbb R^{m}$、缩放 $\Sigma:\mathbb R^{m}\to\mathbb R^{n}$、旋转/镜像 $V:\mathbb R^{n}\to\mathbb R^{n}$。
不失一般性,我们假设 $m = n$ 以及 $U$ 和 $V$ 都是旋转矩阵,则这个过程可以表示为

不难发现,$\mathbf V^{\mathsf H}$ 首先将(可能是退化的)单位球旋转(旋转标准正交基),而后经由 $\mathbf \Sigma$ 将单位圆缩放拉伸成椭圆(超空间中的超椭球),再经由 $\mathbf U$ 将超椭球在 $\mathbb K^{m}$ 空间中旋转。而这个超椭球的各个半轴的长度,就是矩阵 $\mathbf M$ 的奇异值,也就是矩阵 $\mathbf \Sigma$ 对角线上的元素。
SVD 分解的应用
在化学中,有所谓「结构决定性质、性质决定用途」的说法;这反应了一个事物由内而外的特性和人类运用事物的普遍规律。这一规律放在数学上也一样适用。
SVD 将矩阵分解成累加求和的形式,其中每一项的系数即是原矩阵的奇异值。这些奇异值,按之前的几何解释,实际上就是空间超椭球各短轴的长度。现在想象二维平面中一个非常扁的椭圆(离心率非常高),它的长轴远远长于短轴,以至于整个椭圆看起来和一条线段没有什么区别。这时候,如果将椭圆的短轴强行置为零,从直观上看,椭圆退化为线段的过程并不突兀。回到 SVD 分解当中,较大的奇异值反映了矩阵本身的主要特征和信息;较小的奇异值则如例中椭圆非常短的短轴,几乎没有体现矩阵的特征和携带的信息。因此,若我们将 SVD 分解中较小的奇异值强行置为零,则相当于丢弃了矩阵中不重要的一部分信息。
因此,SVD 分解至少有两方面作用:
- 分析了解原矩阵的主要特征和携带的信息(取若干最大的奇异值),这引出了主成分分析(PCA);
- 丢弃忽略原矩阵的次要特征和携带的次要信息(丢弃若干较小的奇异值),这引出了信息有损压缩、矩阵低秩近似等话题。
这两方面的应用实际上是对偶的:因为,按重要度排序之后,一方面我们可以知道哪些信息(奇异值)重要,另一方面我就很自然地就可以丢弃不重要的部分。这里我们以信息的有损压缩为例。
在实际生活和工作当中,很多信息都能被表示为矩阵形式。例如:图像(参见 PIL 简明教程 - 像素操作与图像滤镜)信息,机器学习任务中巨大的特征矩阵等。此处我们循着前文的轨迹,以图像信息的形式直观地展现 SVD 分解在图形压缩中的应用。
首先让我们回顾一下曾经见过的猫咪,它长这样:

经过 SVD 分解之后,RGB 三通道的奇异值值分别形如(代码):
1 | [ 8.29754663e+04 1.43568761e+04 8.28098602e+03 7.94075752e+03 |
当我们从大到小开始截断,丢弃较小的奇异值并重建图像之后,我们就能得到「压缩之后」的图像了。
当只取 1 个奇异值时,重建图像如下。基本啥也看不出。

当只取 5 个奇异值时,重建图像如下。此时已经勉强能看出一只猫咪的形象了。

按照观察,在第 20 个奇异值附近,奇异值的大小有数量级的变化(从 +03 跌落至 +02)。因此,当取 20 个奇异值时,重建图像如下;此时猫咪的形象已经很清晰了。

当取用 50 个奇异值时,重建的图像和原图已经相当接近了。



