始终

不忘初心

0%

谈谈梅森旋转：算法及其爆破

发表于 更新于 分类于
本文字数： 14k 阅读时长 ≈ 26 分钟

现代编程语言，大都在标准库中包含了随机库。例如，C++ 在 C++11 标准中添加了 random 头文件，提供了现代的随机库；Python 则有 random。C++11 的随机库将生成随机数的过程在逻辑上切分成了两个步骤：随机数生成引擎和分布。在学习 C++11 的 random 库时，std::mt19937 这一随机数生成引擎的名字看起来十分奇怪，成功吸引了我的注意力。

查询后得知，std::mt19937 中的 MT 是 Mersenne Twister 的缩写，这是伪随机数生成算法的名字（梅森旋转算法）；而 19937 则取自算法中用到的梅森素数 $2^{19937} - 1$。这里，梅森素数是算法生成伪随机数的循环长度（period），而旋转则说的是算法内部对定长二进制串循环位移的过程。

此篇讲解梅森旋转算法的一些原理，并介绍对其的一个「爆破」方法。

伪随机数发生器质量的度量——$k$-维 $v$-比特准确度

梅森旋转算法（Mersenne Twister Algorithm，简称 MT）是为了解决过去伪随机数发生器（Pseudo-Random Number Generator，简称 PRNG）产生的伪随机数质量不高而提出的新算法。该算法由松本眞（Makoto Matsumoto）和西村拓士（Takuji Nishimura）在 1997 年提出，期间还得到了「算法之神」高德纳（Donald Ervin Knuth）的帮助。

既然 MT 是为了解决过去 PRNG 质量低下的问题，那么首先我们就必须要有一个能够度量 PRNG 质量的方法。否则，「公说公有理婆说婆有理」，我们就无法对 PRNG 作出统一的评价了。

这里介绍评价 PRNG 最严格指标[Tootill et al. 1973][Fushimi and Tezuka 1983][Couture et al. 1993][Tezuka 1995][Tezuka 1994][Tezuka and L'Ecuyer 1991][L'Ecuyer 1996]：$k$-维 $v$-比特准确度（$k$-distributed to $v$-bit accuracy）。

假设某一 PRNG 能够产生周期为 $P$ 的 $w$-比特的随机数序列 $\{\vec x_i\}$；同时，将 $w$-比特的随机数 $\vec x$ 的最高 $v$ 位组成的数记作 $\text{trunc}_v(\vec x)$。现构造如下长度为 $kv$-比特的二进制数

$$\text{PRNG}_{k, v}(i) \overset{\text{def}}{=}(\text{trunc}_v(\vec x_i),\text{trunc}_v(\vec x_{i + 1}),\ldots,\text{trunc}_v(\vec x_{i + k - 1})).$$

由于 $\text{PRNG}_{k, v}(i)$ 是长度为 $kv$-比特的二进制数，所以它可以有 $2^{kv}$ 中不同的取值。若当 $i$ 遍历 $[0, P)$，$\text{PRNG}_{k, v}(i)$ 的取值在这 $2^{kv}$ 中均匀分布。具体来说，$\text{PRNG}_{k, v}(i)$ 落在这 $2^{kv}$ 个取值上的数量完全相等（$\frac{P + 1}{2^{kv}}$），除了全零的取值会少不多不少正好一次（$\frac{P + 1}{2^{kv}} - 1$）。

显而易见，对任意固定的 $v$，若 PRNG 是 $k$-维 $v$-比特准确的，那么必然也是 $(k - 1)$-维 $v$-比特准确的，但不一定是 $(k + 1)$-维 $v$-比特准确的。考虑 $k$ 是有上限的，因此，对于任意固定的 $v$，必然存在最大的 $k = k(v)$ 使得 PRNG 是 $k(v)$-维 $v$-比特准确的。那么，根据定义，显然有 $2^{k(v)v} - 1 \leqslant P$。

$k$-维 $v$-比特准确度也可以有密码学角度的描述：若 PRNG 是 $k$-维 $v$-比特准确的，那么即使已知 PRNG 生成的 $l < k$ 个伪随机数的最高 $v$ 位，也无法推出 PRNG 生成的第 $l + 1$ 个伪随机数的最高 $v$ 位。

根据这样的定义，MT 算法具有非常优良的性能。首先 MT 算法（MT19937）的周期非常长。其周期 $P = 2^{19937} - 1$，要比预估的宇宙可观测的粒子总数（$10^{87}$）还要高出数千个数量级。其次，作为一个 $32$ 比特随机数生成器，MT19937 是 $623$-维 $32$-比特准确的。考虑到 $\bigl\lfloor \frac{19937}{32}\bigr\rfloor = 623$，MT19937 在 $k$-维 $v$-比特准确度上的性能已达到理论上的最大值。因此，MT19937 具有非常优良的性能。

梅森旋转算法的描述

旋转

32 位的梅森旋转算法能够产生周期为 $P$ 的 $w$-比特的随机数序列 $\{\vec x_i\}$；其中 $w = 32$。这也就是说，每一个 $\vec x$ 是一个长度为 32 的行向量，并且其中的每一个元素都是二元数域 $\mathbb{F}_2 \overset{\text{def}}{=} \{0, 1\}$ 中的元素。现在，我们定义如下一些记号，来描述梅森旋转算法是如何进行旋转（线性移位）的。

  • $n$：参与梅森旋转的随机数个数；
  • $r$：$[0, w)$ 之间的整数；
  • $m$：$(0, n]$ 之间的整数；
  • $\mathbf{A}$：$w \times w$ 的常矩阵；
  • $\vec x^{(u)}$：$\vec x$ 的最高 $w - r$ 比特组成的数（低位补零）；
  • $\vec x^{(l)}$：$\vec x$ 的最低 $r$ 比特组成的数（高位补零）。

梅森旋转算法，首先需要根据随机数种子初始化 $n$ 个行向量：

$$\vec x_0, \vec x_1, \ldots, \vec x_{n - 1}.$$

而后根据下式，从 $k = 0$ 开始依次计算 $\vec x_{n}$：

\begin{equation}\vec x_{k + n} \overset{\text{def}}{=} \vec x_{k + m}\oplus \bigl(\vec x_{k}^{(u)}\mid \vec x_{k + 1}^{(l)}\bigr)\mathbf{A}.\label{eq:twister}\end{equation}

其中，$\vec x\mid \vec x'$ 表示两个二进制数按位或；$\vec x\oplus \vec x'$ 表示两个二进制数按位半加（不进位，也就是按位异或）；$\vec x\mathbf A$ 则表示按位半加的矩阵乘法。在 MT 中，$\mathbf A$ 被定义为

$$\begin{pmatrix} & 1 \\ & & 1 \\ & & & \ddots \\ & & & & 1 \\ a_{w - 1} & a_{w - 2} & a_{w - 3} & \cdots & a_0 \end{pmatrix}$$

因此

$$\vec x\mathbf A = \begin{cases}\vec x >> 1& \text{if $x_0 = 0$} \\ (\vec x >> 1)\oplus\vec a& \text{if $x_0 = 1$}\end{cases}.$$

此处，若 $r = 0$，则 MT 退化为 TGFSR (Matsumoto and Kurita 1992, 1994)；若再加上 $\mathbf A = \mathbf I_{w}$，则又从 TGFSR 退化为 GFSR (Lewis and Payne 1973)。

因此，梅森旋转 \ref{eq:twister} 式完全由位运算组成（移位、按位与、按位或、按位异或）。

线性反馈移位寄存器、旋转之名、周期

上一小节我们介绍了 MT 算法当中的「旋转」。但只凭抽象的数学公式（尤其是二进制的逻辑数学），很难看出它为什么是「旋转」。这一节我们首先介绍线性反馈移位寄存器（Linear Feedback Shifting Register，简称 LFSR），看到它是如何「旋转」的；最后再将 LFSR 和 MT 算法当中的旋转步骤统一起来。

反馈移位寄存器是对二进制序列进行等长变换的一种特殊函数。它包括两个部分：

  1. 级。等长変换的长度即是反馈移位寄存器的级。
  2. 反馈函数。若反馈函数是线性的，则称线性反馈移位寄存器；否则是非线性反馈移位寄存器。

一般来说，LFSR 是基于异或运算的。一个 LFSR 的工作步骤是这样的：

  • 将原寄存器状态的最低位作为输出。
  • 执行线性反馈函数；也就是选取其中若干位，从高位到低位迭代异或。
  • 将元寄存器状态向低位移位 1 位，并以上述迭代异或的结果作为填充值填入最高位。

在不断的迭代异或、填充高位的过程中，二进制位在寄存器中循环旋转。这就是「旋转」的来由。

对于一个 4 级的 LFSR 来说，假设其反馈函数是 $f(x) = x^4 + x^2 + x + 1$。则 LFSR 每次从最低位取出结果，将最高位（$x^4$）和倒数第二低位（$x^2$）取异或后，再与最低位（$x$）取异或后，填入移位后的最高位。

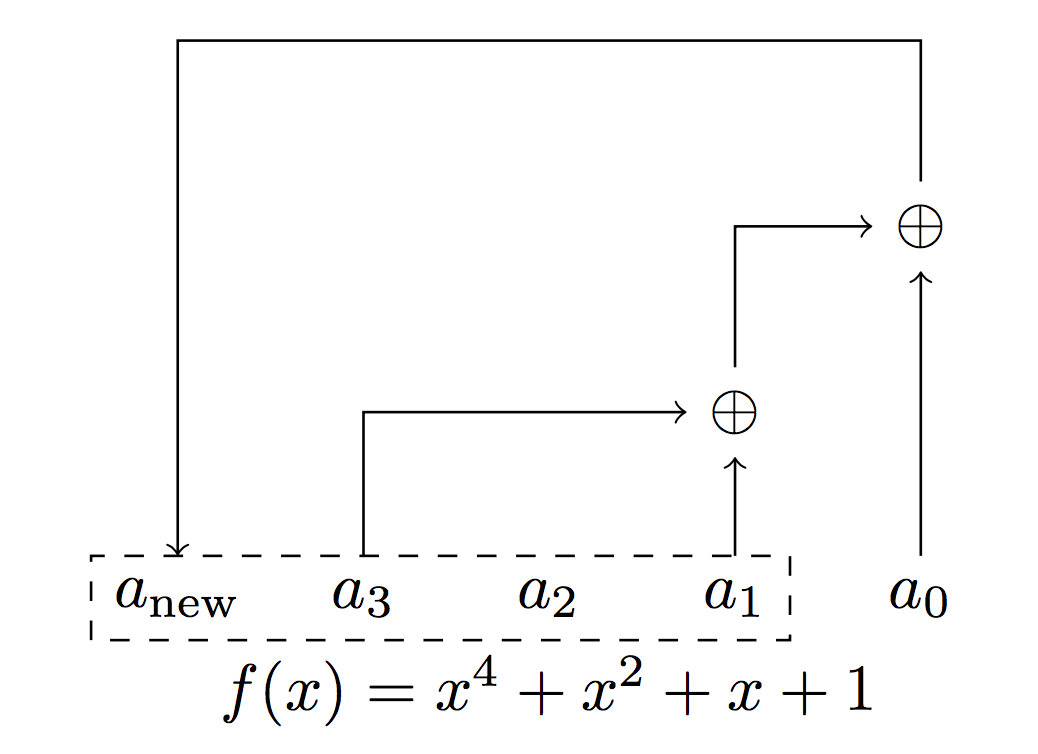
因此，若初始状态为 $(1000)_2$，则有

1
2
3
4
5
6
7
1000
1100
1110
0111
0011
0001
1000  # 复原

如此，我们就构建了一个循环长度为 6 的 LFSR。

考虑一个 $w$ 级的 LFSR，其最多共有 $2^w$ 种状态。又考虑对于异或来说，全零的状态是不可用的（因为不论如何运算都是全零），因此一个 $w$ 级的 LFSR，其有效状态共有 $2^w - 1$ 个。因此，理论上，一个 LFSR 的循环长度最大为 $2^w - 1$。可以证明，当且仅当反馈函数是 $\mathbb F_2$ 上的本原多项式（素多项式）时，LFSR 的循环长度达到最大值。

回过头来看 \ref{eq:twister} 式，不难发现，这其实相当于一个 $nw - r$ 级的线性反馈移位寄存器（取 $\vec x_k^{(u)}$ 的最高 $w - r$ 位与 $\vec x_{k + 1}^{(l)}$ 的最低 $r$ 位进行迭代异或，再经过一个不影响周期的线性变换 $\mathbf A$）。只不过，\ref{eq:twister} 式每一次运算，相当于 LFSR 进行了 $w$ 轮计算。若 $w$ 与 $nw - r$ 互素，那么这一微小的改变是不会影响 LFSR 的周期的。考虑到 LFSR 的计算过程像是在「旋转」，这即是「梅森『旋转』」名字的来由。

对这个等效的 $nw - r$ 级 LFSR 来说，当且仅当反馈函数是 $\mathbb F_2$ 上的本原多项式（素多项式）时，MT 的循环周期长度 $P$ 达到最大值（$2^{nw - r} - 1$）。

提取（tempering）输出

MT19937 有两个主要特性。一是周期很长，达到 $2^{19937} - 1$，二是满足 $623$-维 $32$-比特准确性。上述「旋转」的过程，帮助我们达成了较长的周期。接下来，我们需要将每次旋转的结果提取（tempering）输出，以保证 MT 是 $623$-维 $32$-比特准确的。

提取的方法很简单，只需要将每次旋转得到的输出右乘一个可逆矩阵 $\mathbf T$ 即可。将 $\vec x\mapsto \vec x\mathbf T$ 表述成位运算，则有

\begin{align} \vec y &{}\gets \vec x\oplus (\vec x >> u) \\ \vec y &{}\gets \vec y\oplus ((\vec y << s) \mathop{\mathbf{AND}} \vec b) \\ \vec y &{}\gets \vec y\oplus ((\vec y << t) \mathop{\mathbf{AND}} \vec c) \\ \vec z &{}\gets \vec y\oplus (\vec y >> l) \end{align}

此处，$u$, $s$, $t$, $l$ 是整数参数；$\vec b$ 和 $\vec c$ 是 $w$-比特的整数，用作比特遮罩（bit mask）；最终能得到的 $\vec z$ 即是当前轮次的随机数输出。

算法描述

这样一来，MT 算法的主要有两个部分：旋转、提取。

旋转部分有参数

  • $w$：生成的随机数的二进制长度；
  • $n$：参与旋转的随机数个数（旋转的深度）；
  • $m$：参与旋转的中间项；
  • $r$：$\vec x_{k}^{(u)}$ 和 $\vec x_{k + 1}^{(l)}$ 的切分位置；
  • $\vec a$：矩阵 $\mathbf A$ 的最后一行。

提取部分有参数

  • $u$, $s$, $t$, $l$：整数参数，移位运算的移动距离；
  • $\vec b$, $\vec c$：比特遮罩。

于是，我们得到 MT 算法的完整描述如下。

  1. 常量初始化。
    \begin{align*} \vec{lower} &{}\gets 0 \\ \vec{lower} &{}\gets (\vec{lower} << 1) \mathop{\mathrm{AND}} 1\quad \text{for $r$ times.} \\ \vec{upper} &{}\gets \mathop{\mathrm{COMPL}}\vec{lower} \\ \vec a &{}\gets a_{w - 1}a_{w - 2}\cdots a_{1}a_{0} \\ i &{}\gets 0 \end{align*}
  2. 工作区非零初始化。
    $$\vec x[0], \vec x[1], \ldots, \vec x[n - 1]$$
  3. 旋转
    \begin{align*} \vec t &{}\gets (\vec x[i]\mathop{\mathrm{AND}} \vec{upper}) \mathop{\mathrm{OR}} (\vec x[(i + 1) \mod n]\mathop{\mathrm{AND}} \vec{lower}) \\ \vec x[i] &{}\gets \vec x[(i + m) \mod n]\mathop{\mathrm{XOR}} (\vec t >> 1) \mathop{\mathrm{XOR}} \begin{cases}\vec 0& \text{if $t_0 = 0$}\\ \vec a& \text{otherwise}\end{cases} \end{align*}
  4. 提取输出。
    \begin{align*} \vec y &{}\gets \vec x[i] \\ \vec y &{}\gets \vec y \mathop{\mathbf{XOR}} (\vec y >> u) \\ \vec y &{}\gets \vec y \mathop{\mathbf{XOR}} ((\vec y << s) \mathop{\mathbf{AND}} \vec b) \\ \vec y &{}\gets \vec y \mathop{\mathbf{XOR}} ((\vec y << t) \mathop{\mathbf{AND}} \vec c) \\ \vec y &{}\gets \vec y \mathop{\mathbf{XOR}} (\vec y >> l) \\ &{} \text{output $\vec y$} \end{align*}
  5. 更新循环变量 $i\gets (i + 1)\mod n$，而后跳转至步骤 3 继续进行。

再探梅森旋转

至此，我们已经探索了梅森旋转算法表面上的全部内容：我们已经知道梅森旋转算法是什么，也知道梅森旋转算法为什么这样起名，也有了完整的算法描述。但是，关于梅森旋转算法还有很多深层的问题我们未曾探索。比如说，对于 $n$, $w$ 和 $r$ 的组合，我们是否有必要追求最长周期 $P$ 使得 $P = w^{nw - r} - 1$？又比如说，我们提到 LFSR 取得最长周期的充要条件是反馈函数是 $\mathbb F_{2}$ 上的素多项式，那么怎样验证反馈函数是否是素的？

这一节，我们来讨论这些问题。

关于周期

前文提到，梅森旋转的过程，实际上是对长度为 $nw - r$ 的二进制串做了一个 LFSR 的变体。这里，我们将它记作 $\mathbf B$。

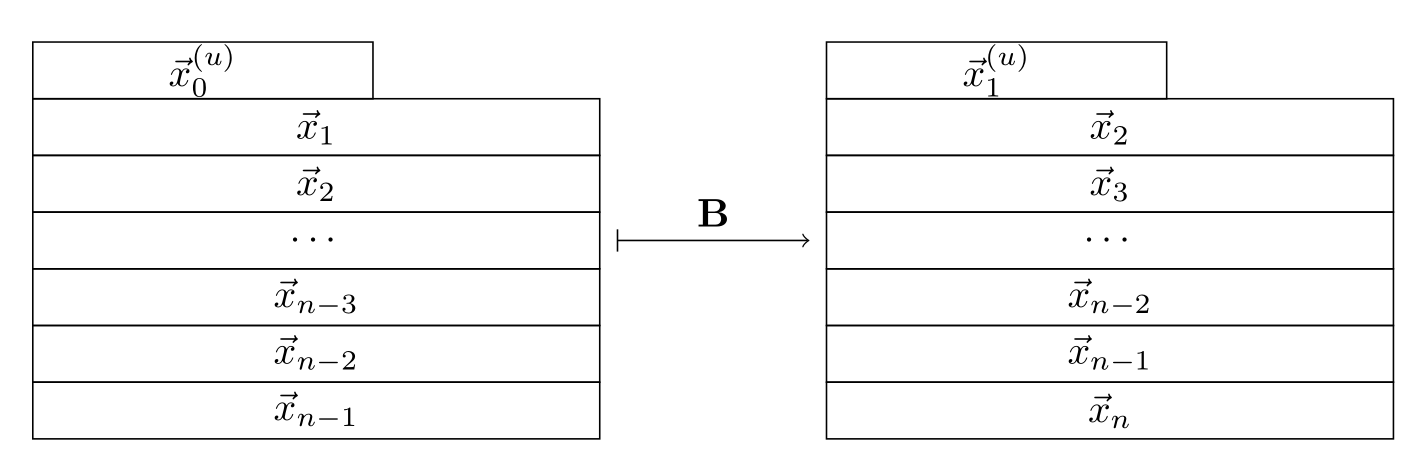
我们已经知道，这个 LFSR 的变体，其周期的上限是 $2^{nw - r} - 1$。这样一来，整个序列的周期达到这一上限就意味着除去全零的状态，整个序列每一种可能状态都被遍历了一遍；而全零的状态则被遍历了 1 遍。考虑在这 $nw - r$ 比特的序列中，$\\{\vec x_n\\}$ 有 $n - 1$ 个完整的 $w$-比特向量；因此，$\\{\vec x_n\\}$ 显然是 $(n - 1)$-维的。这也就是说，选择不同的随机数种子，至多只能改变 ${\vec x_n}$ 序列的起始相位。

这样一来，我们有：当梅森旋转达到最大周期时，若 $n$ 确定，$n - 1$ 就确定了，进而整个序列同分布的维数 $n - 1$ 也就确定了。因此，对于梅森旋转而言，提升维数是很容易的事情。

这即是努力使梅森旋转达到最大周期的意义。

多项式素检测与参数调优

在梅森旋转算法中，反馈函数（$\mathbf B$ 的特征多项式）的素检测是很容易的。这是因为，对于 $p = nw - r$（其中 $p$ 是梅森素数的幂）级的 LFSR 来说，其反馈函数在 $\mathbb F_2$ 上的素检测的复杂度是 $O(p^2)$。这一方面得益于梅森素数的性质，另一方面得益于 MT 是工作在 $\mathbb F_2$ 上的算法。(Matsumoto and Nishimura, 1997) 这一特性的证明，牵扯到很多抽象代数和数论方面的知识；此处我们按下不表，留待后续用专门的文章来证明。

梅森旋转算法中，要实现 PRNG 的最佳性能，需要对旋转和提取两部分参数做细致的调整。调整这部分参数，寻得最优参数组合，是有特定算法可寻的。这部分内容十分繁琐，此处也不表。有兴趣的用户可阅读梅森旋转算法原始论文第四节、第五节。

梅森旋转算法的 Python 实现

此处给出一个 Python 实现的梅森旋转算法（mt19937），为后续对算法的「爆破」提供素材。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#! coding: utf-8

class MersenneTwister:
    __n = 624
    __m = 397
    __a = 0x9908b0df
    __b = 0x9d2c5680
    __c = 0xefc60000
    __kInitOperand = 0x6c078965
    __kMaxBits = 0xffffffff
    __kUpperBits = 0x80000000
    __kLowerBits = 0x7fffffff

    def __init__(self, seed = 0):
        self.__register = [0] * self.__n
        self.__state = 0

        self.__register[0] = seed
        for i in range(1, self.__n):
            prev = self.__register[i - 1]
            temp = self.__kInitOperand * (prev ^ (prev >> 30)) + i
            self.__register[i] = temp & self.__kMaxBits

    def __twister(self):
        for i in range(self.__n):
            y = (self.__register[i] & self.__kUpperBits) + \
                    (self.__register[(i + 1) % self.__n] & self.__kLowerBits)
            self.__register[i] = self.__register[(i + self.__m) % self.__n] ^ (y >> 1)
            if y % 2:
                self.__register[i] ^= self.__a
        return None

    def __temper(self):
        if self.__state == 0:
            self.__twister()

        y = self.__register[self.__state]
        y = y ^ (y >> 11)
        y = y ^ (y << 7) & self.__b
        y = y ^ (y << 15) & self.__c
        y = y ^ (y >> 18)

        self.__state = (self.__state + 1) % self.__n

        return y

    def __call__(self):
        return self.__temper()

    def load_register(self, register):
        self.__state = 0
        self.__register = register

if __name__ == "__main__":
    mt = MersenneTwister(0)
    tank = set()
    kLen = 100
    for i in range(kLen):
        t = mt()
        tank.add(t)
        print(t)
    print(len(tank) == kLen)

爆破梅森旋转算法

梅森旋转算法的设计目的是优秀的伪随机数发生算法，而不是产生密码学上安全的随机数。从梅森旋转算法的结构上说，其提取算法 __temper 完全基于二进制的按位异或；而二进制按位异或是可逆的，故而 __temper 是可逆的。这就意味着，攻击者可以从梅森旋转算法的输出，逆推出产生该输出的内部寄存器状态 __register[__state]。若攻击者能够获得连续的至少 __n 个寄存器状态，那么攻击者就能预测出接下来的随机数序列。

现在我们遵循这个思路，爆破梅森旋转算法。

逆向 __temper

我们以向右移位后异或为例，首先观察原函数。

1
2
3
4
def right_shift_xor(value, shift):
    result = value
    result ^= (result >> shift)
    return result

简单起见，我们观察一个 8 位二进制数，右移 3 位后异或的过程。

1
2
3
value:    1101 0010
shifted:  0001 1010 # 010 (>> 3)
result:   1100 1000

首先，观察到 result 的最高 shift 位与 value 的最高 shift 位是一样的。因此，在 result 的基础上，我们可以将其与一个二进制遮罩取与，得到 value 的最高 shift 位。这个遮罩应该是：1111 1111 << (8 - 3) = 1110 0000。于是我们得到 1100 0000。

其次，注意到对于异或运算有如下事实：a ^ b ^ b = a。依靠二进制遮罩，我们已经获得了 value 的最高 shift 位。因此，我们也就能得到 shifted 的最高 2 * shift 位。它应该是 1100 0000 >> 3 = 0001 1000。将其与 result 取异或，则能得到 value 的最高 2 * shift 位。于是我们得到 1101 0000。

如此往复，即可复原 value。据此有代码

1
2
3
4
5
6
7
8
9
def inverse_right_shift_xor(value, shift):
    i, result = 0, 0
    while i * shift < 32:
        part_mask = ((0xffffffff << (32 - shift)) & 0xffffffff) >> (i * shift)
        part = value & part_mask
        value ^= part >> shift
        result |= part
        i += 1
    return result

对左移后取异或，也有类似分析。于是，得到对 __temper 的完整求逆代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class TemperInverser:
    __b = 0x9d2c5680
    __c = 0xefc60000
    __kMaxBits = 0xffffffff

    def __inverse_right_shift_xor(self, value, shift):
        i, result = 0, 0
        while i * shift < 32:
            part_mask = ((self.__kMaxBits << (32 - shift)) & self.__kMaxBits) >> (i * shift)
            part = value & part_mask
            value ^= part >> shift
            result |= part
            i += 1
        return result

    def __inverse_left_shift_xor(self, value, shift, mask):
        i, result = 0, 0
        while i * shift < 32:
            part_mask = (self.__kMaxBits >> (32 - shift)) << (i * shift)
            part = value & part_mask
            value ^= (part << shift) & mask
            result |= part
            i += 1
        return result

    def __inverse_temper(self, tempered):
        value = tempered
        value = self.__inverse_right_shift_xor(value, 18)
        value = self.__inverse_left_shift_xor(value, 15, self.__c)
        value = self.__inverse_left_shift_xor(value, 7, self.__b)
        value = self.__inverse_right_shift_xor(value, 11)
        return value

    def __call__(self, tempered):
        return self.__inverse_temper(tempered)

爆破

逆向 __temper() 之后，只要获得足够的状态，即可构建出梅森旋转内部的寄存器状态。因此有如下验证代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class MersenneTwisterCracker:
    __n = 624

    def __init__(self, mt_obj):
        inverser  = TemperInverser()
        register  = [inverser(mt_obj()) for i in range(self.__n)]
        self.__mt = MersenneTwister(0)
        self.__mt.load_register(register)

    def __call__(self):
        return self.__mt()

if __name__ == "__main__":
    mt  = MersenneTwister(0)
    for i in range(100):
        mt()
    mtc = MersenneTwisterCracker(mt)
    for i in range(100):
        assert(mt() == mtc())

运行后，Python 没有抛出异常，顺利退出。这说明 mtc 已能够成功预测 mt 之后的任意顺序输出。

总结

梅森旋转算法，是一个优秀的伪随机数发生算法。在伪随机数的评价体系中，它是一个相当优秀的算法：周期长、均匀性好、速度快（基本都是位运算）。在条件允可的情形下，若有使用随机数的需求，应首先考虑梅森旋转算法。

同时也应该注意到，梅森旋转算法不是为了密码学随机而设计的——在获得足够连续输出的情况下，梅森旋转算法接下来的输出值是可以准确预测的。梅森旋转算法容易被爆破的根源在于，其提取输出函数是可逆的，因此暴露了其内部状态。若要产生密码学上的随机数，可考虑在梅森旋转算法之后，拼接一值得信赖的单向杂凑函数（如 sha256）。否则，若直接用梅森旋转算法的输出值作密码学用途，则有信息泄露的风险，应引起注意。

错误应用梅森旋转算法，导致高危漏洞的一个典型是 Discuz! 的密码重置漏洞。

扩展阅读：梅森旋转算法的原始论文

俗话说，投资效率是最好的投资。 如果您感觉我的文章质量不错，读后收获很大，预计能为您提高 10% 的工作效率，不妨小额捐助我一下，让我有动力继续写出更多好文章。