今天在讨论神经网络中的激活函数时,陆同学提出 Sigmoid 函数的输出不是以零为中心的(non-zero-centered),这会导致神经网络收敛较慢。关于这一点,过去我只是将其记下,却并未理解背后的原因。此篇谈谈背后的原因。
神经元
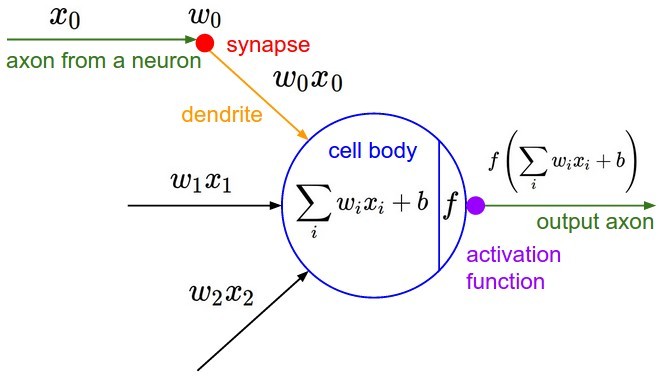
如图是神经网络中一个典型的神经元设计,它完全仿照人类大脑中神经元之间传递数据的模式设计。大脑中,神经元通过若干树突(dendrite)的突触(synapse),接受其他神经元的轴突(axon)或树突传递来的消息,而后经过处理再由轴突输出。
在这里,诸 $x_i$ 是其他神经元的轴突传来的消息,诸 $w_i$ 是突触对消息的影响,诸 $w_ix_i$ 则是神经元树突上传递的消息。这些消息经由神经元整合后($z(\vec x; \vec w, b) = \sum_iw_ix_i + b$)再激活输出($f(z)$)。这里,整合的过程是线性加权的过程,各输入特征 $x_i$ 之间没有相互作用。激活函数(active function)一般来说则是非线性的,各输入特征 $x_i$ 在此处相互作用。
Sigmoid 与 tanh
此篇集中讨论激活函数输出是否以零为中心的问题,因而不对激活函数做过多的介绍,而只讨论 Sigmoid 与 tanh 两个激活函数。
Sigmoid 函数
Sigmoid 函数的一般形式是
$$\sigma(x; a) = \frac{1}{1 + \mathrm{e}^{-ax}}.$$
这里,参数 $a$ 控制 Sigmoid 函数的形状,对函数基本性质没有太大的影响。在神经网络中,一般设置 $a = 1$,直接省略。
Sigmoid 函数的导数很好求
$$\sigma'(x) = \sigma(x)\bigl(1 - \sigma(x)\bigr).$$
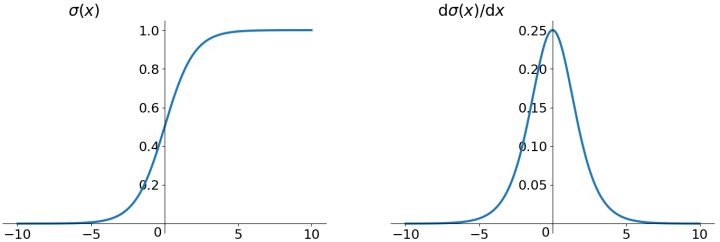
tanh 函数
tanh 函数全称 Hyperbolic Tangent,即双曲正切函数。它的表达式是
$$\tanh(x) = 2\sigma(2x) - 1 = \frac{\mathrm{e}^{x} - \mathrm{e}^{-x}}{\mathrm{e}^{x} + \mathrm{e}^{-x}}.$$
双曲正切函数的导数也很好求
$$\tanh'(x) = 1 - \tanh^2(x).$$
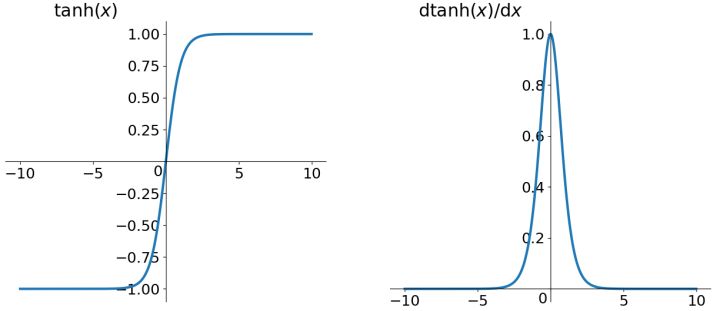
一些性质
Sigmoid 和 tanh 两个函数非常相似,具有不少相同的性质。简单罗列如下
- 优点:平滑
- 优点:易于求导
- 缺点:幂运算相对耗时
- 缺点:导数值小于 $1$,反向传播易导致梯度消失(Gradient Vanishing)
对于 Sigmoid 函数来说,它的值域是 $(0, 1)$,因此又有如下特点
- 优点:可以作为概率,辅助模型解释
- 缺点:输出值不以零为中心,可能导致模型收敛速度慢
此篇重点讲 Sigmoid 函数输出值不以零为中心的这一缺点。
收敛速度
这里首先需要给收敛速度做一个诠释。模型的最优解即是模型参数的最优解。通过逐轮迭代,模型参数会被更新到接近其最优解。这一过程中,迭代轮次多,则我们说模型收敛速度慢;反之,迭代轮次少,则我们说模型收敛速度快。
参数更新
深度学习一般的学习方法是反向传播。简单来说,就是通过链式法则,求解全局损失函数 $L(\vec x)$ 对某一参数 $w$ 的偏导数(梯度);而后辅以学习率 $\eta$,向梯度的反方向更新参数 $w$。
$$w \gets w - \eta\cdot\frac{\partial L}{\partial w}.$$
考虑学习率 $\eta$ 是全局设置的超参数,参数更新的核心步骤即是计算 $\frac{\partial L}{\partial w}$。再考虑到对于某个神经元来说,其输入与输出的关系是
$$f(\vec x; \vec w, b) = f(z) = f\Bigl(\sum_iw_ix_i + b\Bigr).$$
因此,对于参数 $w_i$ 来说,
$$\frac{\partial L}{\partial w_i} = \frac{\partial L}{\partial f}\frac{\partial f}{\partial z}\frac{\partial z}{\partial w_i} = x_i \cdot \frac{\partial L}{\partial f}\frac{\partial f}{\partial z}.$$
因此,参数的更新步骤变为
$$w_i \gets w_i - \eta x_i\cdot \frac{\partial L}{\partial f}\frac{\partial f}{\partial z}.$$
更新方向
由于 $w_i$ 是上一轮迭代的结果,此处可视为常数,而 $\eta$ 是模型超参数,参数 $w_i$ 的更新方向实际上由 $x_i\cdot \frac{\partial L}{\partial f}\frac{\partial f}{\partial z}$ 的符号决定。
考虑下标不同的两个参数 $w_i$ 和 $w_j$,它们的更新方向分别由以下两式的符号决定:
$$\begin{cases}x_i\cdot \frac{\partial L}{\partial f}\frac{\partial f}{\partial z}, \\ x_j\cdot \frac{\partial L}{\partial f}\frac{\partial f}{\partial z}.\end{cases}$$
又考虑到 $\frac{\partial L}{\partial f}\frac{\partial f}{\partial z}$ 对于所有的 $w_i$ 来说是常数,因此各个 $w_i$ 更新方向之间的差异,完全由对应的输入值 $x_i$ 的符号的差异决定。例如说,若 $x_i$ 与 $x_j$ 的符号相同,则 $w_i$ 和 $w_j$ 更新方向就相同;反之,若 $x_i$ 与 $x_j$ 的符号相反,则 $w_i$ 和 $w_j$ 更新方向就相反。
以零为中心的影响
至此,为了描述方便,我们以二维的情况为例。亦即,神经元描述为
$$f(\vec x; \vec w, b) = f\bigl(w_0x_0 + w_1x_1 + b\bigr).$$
现在假设,参数 $w_0$, $w_1$ 的最优解 $w_0^{*}$, $w_1^{*}$ 满足条件
$$\begin{cases}w_0 < w_0^{*}, \\ w_1\geqslant w_1^{*}.\end{cases}$$
这也就是说,我们希望 $w_0$ 适当增大,但希望 $w_1$ 适当减小。考虑到上一小节提到的更新方向的问题,如果想要「一次到位」这就必然要求 $x_0$ 和 $x_1$ 符号相反。
但在 Sigmoid 函数中,输出值恒为正。这也就是说,如果上一级神经元采用 Sigmoid 函数作为激活函数,那么我们无法做到 $x_0$ 和 $x_1$ 符号相反。此时,模型为了收敛,不得不向逆风前行的风助力帆船一样,走 Z 字形逼近最优解。
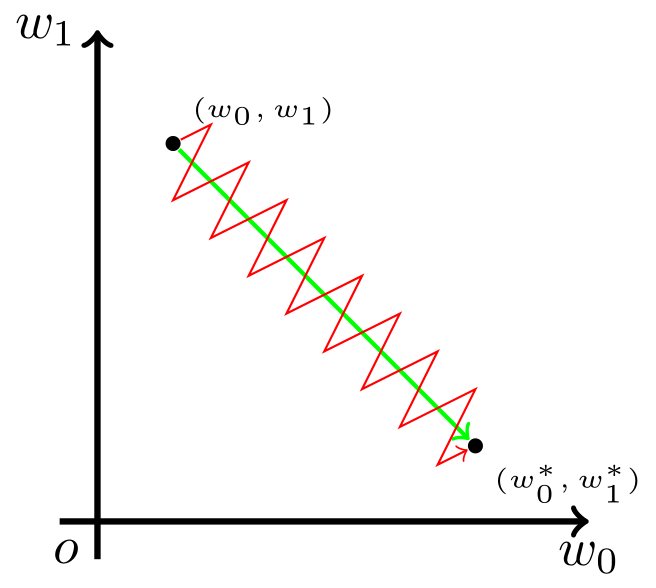
如图,模型参数走绿色箭头能够最快收敛,但由于输入值的符号总是为正,所以模型参数可能走类似红色折线的箭头。如此一来,使用 Sigmoid 函数作为激活函数的神经网络,收敛速度就会慢上不少了。


