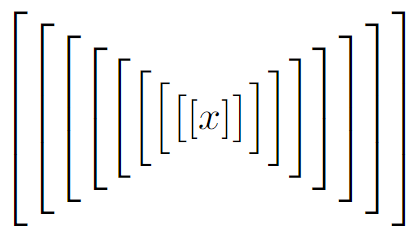LaTeX 黑魔法（六）：使用比逼格更逼格的定界符

通常，我们建议在 LaTeX 中使用 LaTeX 提供的 \big, \Big, \bigg, \Bigg 一系列命令，代替 TeX 默认的 \left 和 \right 来调整定界符的大小。然而，尽管最大提供了 \Bigg 的命令，但有时候仍然不够用。

此篇介绍如何定义 \biggg, \Biggg, \bigggg 和 \Bigggg 系列命令。我们的口号是「比逼格更逼格」（bigger than bigger）！

挖掘代码

\big 系列命令

要定义更大的定界符修饰，就必须搞清楚 \big 系列命令是如何定义的。首先，我们使用 kpsewhich amsmath.sty 找到 amsmath.sty 在系统中的路径。而后打开样式文件，搜寻 \big 的定义。

\renewcommand{\big}{\bBigg@\@ne}
\renewcommand{\Big}{\bBigg@{1.5}}
\renewcommand{\bigg}{\bBigg@\tw@}
\renewcommand{\Bigg}{\bBigg@{2.5}}

\bBigg@ 命令

显而易见，核心是 \bBigg@ 这个命令。它可以根据其后第一个 token 决定定界符的放大程度。注意，这里 \@ne 表示 {1}，而 \tw@ 表示 {2}——这是令人讨厌的 LaTeX 内核编程 trick。于是我们继续去寻找 \bBigg@ 的定义。

\def\bBigg@#1#2{%
  {\@mathmeasure\z@{\nulldelimiterspace\z@}%
     {\left#2\vcenter to#1\big@size{}\right.}%
   \box\z@}}

很显然，\bBigg@ 命令内部也是通过 TeX 原始的 \left 和 \right 命令来调整定界符（#2）的大小的。不过，它还额外处理了左右的空距。这里我们知道就行了，不去深究。

\bigl 和 \bigr 系列命令

接下来我们继续挖掘 \bigl 和 \bigr 系列命令的定义。它们定义在 LaTeX2e 内核当中，因此我们通过执行 texdoc source2e 就能看到它们的定义了。

\def\bigl{\mathopen\big}
\def\bigm{\mathrel\big}
\def\bigr{\mathclose\big}
\def\Bigl{\mathopen\Big}
\def\Bigm{\mathrel\Big}
\def\Bigr{\mathclose\Big}
\def\biggl{\mathopen\bigg}
\def\biggm{\mathrel\bigg}
\def\biggr{\mathclose\bigg}
\def\Biggl{\mathopen\Bigg}
\def\Biggm{\mathrel\Bigg}
\def\Biggr{\mathclose\Bigg}

很显然，它们就只是用 \mathopen, \mathrel 和 \mathclose 宏来修饰了一下对应的定界符修饰命令。

改造

据此，我们可以定义更有逼格的定界符修饰命令了。

% \RequirePackage{amsmath}

\newcommand{\biggg}{\bBigg@{3}}
\def\bigggl{\mathopen\biggg}
\def\bigggm{\mathrel\biggg}
\def\bigggr{\mathclose\biggg}
\newcommand{\Biggg}{\bBigg@{3.5}}
\def\Bigggl{\mathopen\Biggg}
\def\Bigggm{\mathrel\Biggg}
\def\Bigggr{\mathclose\Biggg}
\newcommand{\bigggg}{\bBigg@{4}}
\def\biggggl{\mathopen\bigggg}
\def\biggggm{\mathrel\bigggg}
\def\biggggr{\mathclose\bigggg}
\newcommand{\Bigggg}{\bBigg@{4.5}}
\def\Biggggl{\mathopen\Bigggg}
\def\Biggggm{\mathrel\Bigggg}
\def\Biggggr{\mathclose\Bigggg}

注意，这段代码在普通的 LaTeX 文档中，需要使用 \makeatletter 和 \makeatother 来改变 @ 字符的分类码，以便正确定义命令。

接下来我们实际使用看看。

\documentclass{article}

\usepackage{amsmath}

\makeatletter
\newcommand{\biggg}{\bBigg@{3}}
\def\bigggl{\mathopen\biggg}
\def\bigggm{\mathrel\biggg}
\def\bigggr{\mathclose\biggg}
\newcommand{\Biggg}{\bBigg@{3.5}}
\def\Bigggl{\mathopen\Biggg}
\def\Bigggm{\mathrel\Biggg}
\def\Bigggr{\mathclose\Biggg}
\newcommand{\bigggg}{\bBigg@{4}}
\def\biggggl{\mathopen\bigggg}
\def\biggggm{\mathrel\bigggg}
\def\biggggr{\mathclose\bigggg}
\newcommand{\Bigggg}{\bBigg@{4.5}}
\def\Biggggl{\mathopen\Bigggg}
\def\Biggggm{\mathrel\Bigggg}
\def\Biggggr{\mathclose\Bigggg}
\makeatother

\begin{document}

\[
    \Biggggl[\biggggl[\Bigggl[\bigggl[\Biggl[\biggl[\Bigl[\bigl[[ x ]\bigr]\Bigr]\biggr]\Biggr]\bigggr]\Bigggr]\biggggr]\Biggggr]
\]

\end{document}