分类问题是机器学习领域的一大类问题,二分类问题又是其中最为基础的一种。在评价模型性能时,机器学习领域延伸出了很多评价指标。这篇文章简单梳理一下这些指标。
混淆矩阵(confusion matrix)
二分类模型的基本工作是这样的:
- 将样本
$\{\vec x, y\}$输入二分类模型$\mathcal C$,得到模型输出得分$s$; - 将模型输出得分
$s$映射为最终结果$\hat y = M(s)$。
对于给定的模型 $\mathcal C$ 和映射函数 $M(\cdot)$,根据样本真实分类 $y$ 和模型预测分类 $\hat y$ 的组合,定义如下四种情况:
- 真阳性(True Positive,简称:TP):表示样本是阳性
$y = 1$,并且模型也预测为阳性$\hat y = 1$。 - 假阳性(False Positive,简称:FP):表示样本是阴性
$y = 0$,但模型预测为阳性$\hat y = 1$。 - 真阴性(True Negative,简称:TN):表示样本是阴性
$y = 0$,并且模型也预测为阴性$\hat y = 0$。 - 假阴性(False Negative,简称:FN):表示样本是阳性
$y = 1$,但模型预测为阴性$\hat y = 0$。
又根据样本真实分类 $y$ 和模型预测分类 $\hat y$ 的实际情况,定义如下四个变量:
$P = TP + FN$:表示所有真实分类为阳性的样本的数量。$N = FP + TN$:表示所有真实分类为阴性的样本的数量。$P' = TP + FP$:表示所有预测分类为阳性的样本的数量。$N' = TN + FN$:表示所有预测分类为阴性的样本的数量。
于是可绘制如下混淆矩阵:
| 真实值 | 总 数 | |||
|---|---|---|---|---|
| 1 | 0 | |||
| 预 测 输 出 |
1 | 真阳性 (TP) |
假阳性 (FP) |
P' |
| 0 | 假阴性 (FN) |
真阴性 (TN) |
N' | |
| 总数 | P | N | ||
由混淆矩阵衍生的指标
混淆矩阵是二分类模型与其数据相互作用得到的最基本的结果。建立在混淆矩阵之上,我们可以定义出一系列的指标,来衡量二分类模型的性能。这里对常见的指标及需要关注的要点罗列如下。
- 真阳性率(true positive rate,TPR)/敏感度(sensitivity)/召回率(recall rate):在二分类问题中,真阳性率、敏感度和召回率三个名词对应着同一个概念;它表示正样本中被预测为正样本的占比。一般而言,它的值越大意味着模型性能越好。其计算公式是
$TPR = TP / P = TP / (TP + FN).$ - 真阴性率(true negative rate,TNR)/特异度(specificity):在二分类问题中,真阴性率和特异度对应着同一个概念;它表示负样本中被预测为负样本的占比。一般而言,它的值越大意味着模型性能越好。其计算公式是
$TNR = TN / N = TN / (TN + FP).$ - 假阳性率(false positive rate,FPR):它表示负样本中被错误地预测为正样本的占比。一般而言,它的值越小意味着模型性能越好。其计算公式是
$FPR = FP / N = FP / (TN + FP) = 1 - TNR.$ - 假阴性率(false negative rate,FNR):它表示正样本中被错误滴预测为负样本的占比。一般而言,它的值越小意味着模型性能越好。其计算公式是
$FNR = FN / P = FN / (TP + FN) = 1 - TPR.$ - 阳性预测值(positive predictive value,PPV)/精确率(percision):它表示被预测为正的样本中正样本的占比。在二分类问题中,阳性预测值和精确率对应着同一个概念;一般而言,它的值越大意味着模型性能越好。其计算公式是
$PPV = TP / (TP + FP) = TP / P'.$ - 阴性预测值(negative predictive value,NPV):它表示被预测为负的样本中负样本的占比。一般而言,它的值越大意味着模型性能越好。其计算公式是
$NPV = TN / (TN + FN) = TN / N'.$ - 假发现率(false detective rate,FDR):它表示被预测为正的样本中负样本的占比。一般而言,它的值越小意味着模型性能越好。其计算公式是
$FDR = FP / (TP + FP) = FP / P' = 1 - PPV.$ - 准确率(accuracy,ACC):它表示全体样本中预测正确的样本的占比。一般而言,它的值越大意味着模型性能越好。其计算公式是
$ACC = (TP + TN) / (P + N).$ - F1 值(F1-score):它是召回率(真阳性率)和精确率(阳性预测值)的调和平均。一般而言,它的值越大意味着模型性能越好。其计算公式是
$F1 = 2TP / (P + P').$ - 约登指数(Youden's J statistic):一般而言,它的值越大意味着模型性能越好。其计算公式是
$J = TPR + TNR - 1.$
准确率悖论(Accuracy Paradox)
准确率表示全体样本中,模型预测正确的样本之占比。这是一个非常 intuitive 的指标,和我们一般的认知很相符。但准确率有一个很大的问题:当正负例极不平衡时,即当 $P \gg N$ 或 $N \gg P$ 时,准确率会被样本量占优的类别主导从而失真。一般我们认为正例是重要的,于是这个问题在负例数量远多于正例数量时,显得尤为严重。欺诈检测、癌症检测等场合,均属于这种情况。
举个栗子。假设验证集中共有 100 个样本,其中有 95 个负例和 5 个正例。若模型对所有输入都认定为负例,则这种情况下有 $ACC = (TP + TN) / (P + N) = (0 + 95) / (5 +95) = 0.95$。看起来准确率很高,但这个模型一个正例都分辨不出来,没有实际价值。
单独用 TPR、TNR、FPR、FNR、PPV、NPV、FDR 这些指标,也会遇到类似的困难。
召回率(真阳性率,TPR)、精确率(阳性预测值,PPV)与 F1 值
计算召回率和精确率时的分子都是 TP,不同在于分母。召回率的分母是 $P$,而精确率的分母是 $P'$。这也就是说,召回率是相对真实样本而言的,精确率是相对模型预测为正例的样本而言的。
举个栗子。
- 假设验证集当中有 100 个正例,你的模型将这 100 个正例中的 40 个预测为正例,则你的模型的召回率是 40%。
- 假设你的模型一共预测了 50 个正例,其中 40 个确实是正例(还有 10 个是负例,即 FP 的情形),则你的模型精确率是 80%。
显然,若要提高召回率,则模型会变得「贪婪」,于是犯错的可能性就会变大,也就是精确率下降;若要提高精确率,则模型会变得「保守」,此时模型能够覆盖的正例就少,于是召回率下降。考虑到召回率和精确率之间「跷跷板」的关系,人们发明了 F1 值这个指标,并将其定义为召回率和精确率的调和平均数,从而能够比较容易地在召回率和精确率方面取得平衡:
$$F1 = \frac{2}{\frac{1}{TPR} + \frac{1}{PPV}} = \frac{2TP}{P + P'}.$$
敏感度(真阳性率,TPR)、特异度(真阴性率,TNR)与约登指数
从数学上将,召回率和精确率之间跷跷板一般的关系来自于精确率计算的分母是 $P'$ 而非 $P$。因为当模型发生变化的时候,$P'$ 就会发生变化。所以你无法在提升召回率的时候,保证精确率不变;反之亦然。
既然如此,我们寻找分母为 $P$ 或 $N$ 的指标,是否就能解决这个问题了呢?按照这个思路,人们定义了敏感度和特异度的概念。
- 敏感度就是召回率,它是真阳性率的有一个马甲。
- 特异度是模型在负例上的召回率,因此它是真阴性率的马甲。
因为敏感度和特异度分别是以验证集中正例数量和负例数量为分母的,所以它们:
- 不存在必然的跷跷板关系;
- 不受不平衡数据的影响。
这就「很理中客」了嘛。为了统一考量模型的敏感度和特异度,即为了统一考量模型在正负例上的召回率,人们又定义了约登指数。
$$J = TPR + TNR - 1.$$
曲线及其 AUC(Area under Curve,曲线下面积)
上面的讨论都基于一个假设,即映射函数 $M(\cdot)$ 是确定的。如果映射函数发生变化,模型对样本的最终预测 $\hat y$ 就会发生变化,进而影响到混淆矩阵,最终影响到各个评价指标。因此,在这个意义下,对于确定的模型,各个指标将是映射函数的函数。
一般来说,对于二分类问题,映射函数是一个简单的分段函数。于是,各个指标将是分段阈值 $t$ 的函数。
$$M(s) = \begin{cases} 1 & s > t, \\ 0 & \text{otherwise}. \end{cases}$$
对于需要取舍的指标对,我们可以做如下操作,得到一条曲线(折线):
- 逐渐改变阈值
$t$,得到序列$\bigl\{\bigl(A(t), B(t)\bigr)\bigr\}$。 - 将指标 A 和指标 B 分别作为平面直角坐标系的横轴和纵轴。
- 将序列对应的点,绘制在平面直角坐标系中。
- 顺序连接这些点。
对于真阳性率(敏感度,召回率)和假阳性率(1 - 特异度),这条曲线是接收者操作特征曲线(receiver operating characteristic curve)。对于召回率和精确率,这条曲线是精确率-召回率曲线(PR-Curve)。
接收者操作特征曲线(receiver operating characteristic curve, ROC)
一条典型的 ROC 如下图所示。
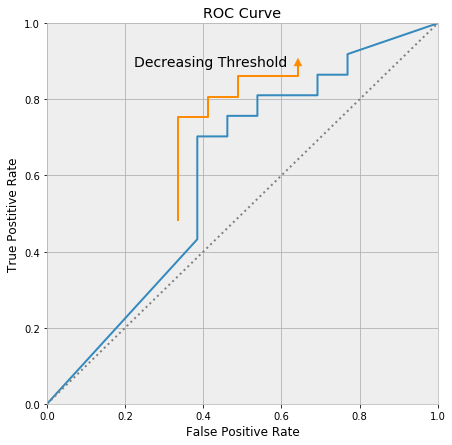
这里,横坐标代表假阳性率 FPR,它是阈值 $t$ 的函数,我们记作 $F(t)$;纵坐标代表真阳性率 TPR,它也是阈值 $t$ 的函数,我们记作 $T(t)$。从图中很明显能看出 FPR 和 TPR 之间「鱼和熊掌不可兼得」的关系。曲线下面积(AUC)越大,也就是曲线约接近左上角,说明模型就越理想。那么 ROC 的 AUC 是什么含义呢?
我们将 FPR 看做是一个累积分布函数,即
$$F(t) = P(\hat y \geqslant t \mid y = 0),$$
因此 FPR 相对 $t$ 的偏导数应当是一个概率密度函数,即
$$\frac{\partial F(t)}{\partial t} = P(\hat y = t \mid y = 0).$$
我们将 TPR 看做是 FPR 的函数,即 $T(t) = T(F) = T(F^{-1}(F(t)))$。因此有
$$\begin{aligned} \text{AUC} = {}& \int_{0}^{1} T(F)\,\mathop{}\mathrm{d}F \\ = {}& \int_{0}^{1} P(\hat y > t \mid y = 1)\cdot\frac{\partial F(t)}{\partial t}\,\mathop{}\mathrm{d}t \\ = {}& \int_{0}^{1} P(\hat y > t \mid y = 1)\cdot P(\hat y' = t \mid y' = 0)\,\mathop{}\mathrm{d}t \\ = {}& \int_{0}^{1} P(\hat y > t \wedge \hat y' = t \mid y = 1 \wedge y' = 0)\,\mathop{}\mathrm{d}t \\ = {}& \int_{0}^{1} P(\hat y > \hat y' \wedge \hat y' = t \mid y = 1 \wedge y' = 0)\,\mathop{}\mathrm{d}t \\ = {}& P(\hat y > \hat y' \mid y = 1 \wedge y' = 0). \\ \end{aligned}$$
于是我们知道,ROC 的 AUC 表示任选正负例对 $\bigl((\vec x_1, y_1 = 1), (\vec x_2, y_2 = 0)\bigr)$,模型输出得分中,正例得分大于负例得分的概率 $P\bigl(\mathcal C(\vec x_1) > \mathcal C(\vec x_2)\bigr)$。换言之,ROC 的 AUC 反映了模型的排序能力。这在 CTR 预估排序的场景下,非常有用。
关于这一点,这里有一个有趣的集合解释。
另外,值得一提的是,一般默认的 AUC 指的是 AUC of ROC。
精确率-召回率曲线(precision-recall curve, PR-Curve)
一条典型的 PR-Curve 如下图所示。
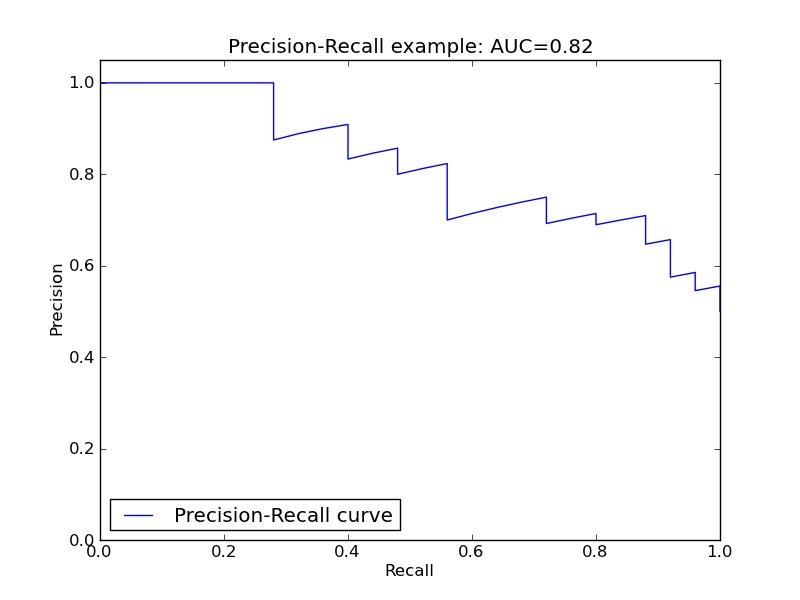
从中很明显能看出来之前说的「跷跷板」关系。曲线下面积(AUC)越大,也就是曲线约接近右上角,说明模型就越理想。但这种情况,在实际工作中基本是不可能出现的。因此我们需要根据实际问题进行取舍(确定一个合适的 $t$)。
对于正例显著少于负例的情况,人们往往追求尽可能高的召回率。因此,可以预先设定一个精确率下限,然后在这个下限之上,寻找召回率最高的点。比如在上图中,若设定可接受的最低精确率是 0.8,则召回率最高大约是 0.55;若设定可接受的最低精确率是 0.6,则召回率最高大约是 0.92。对于正例显著多于负例的情况,人们往往追求尽可能高的精确率。此时可以反向操作,选取合适的 $t$。
同样的问题:那么 PR-Curve 的 AUC 是什么含义呢?利用类似的思路可得:PR-Curve 的 AUC 表示任选一个正例 $(\vec x_1, y_1 = 1)$,而后任选一个满足 $\mathcal C(\vec x_2) > \mathcal C(\vec x_1)$ 的样本 $(\vec x_2, y_2)$,该样本为正样本的概率 $P\bigl(y_2 = 1 \mid y_1 = 1 \wedge \mathcal C(\vec x_2) > \mathcal C(\vec x_1)\bigr)$。
ROC 与 PR-Curve 的比较
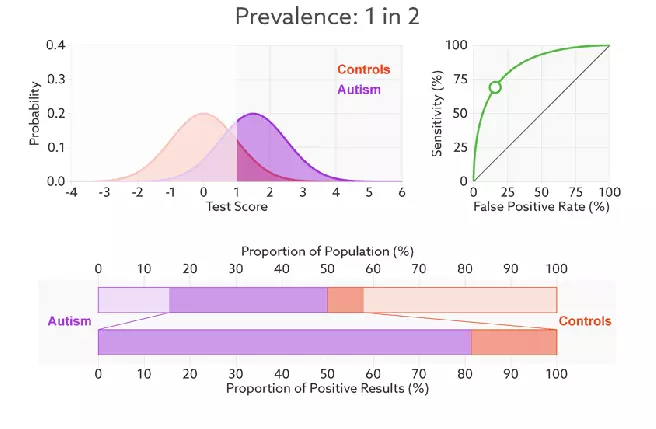
由于 ROC 的横纵坐标分别表示 FPR 和 TPR,二者的分母完全隔开,从而使得 AUC of ROC 不受正负样本比例的影响(如上图所示)。这看起来是个好事,因为它在倾斜的数据集上依然保持了稳定的物理意义(类似准确率)。但是,另一方面,这说明在负例数量远大于正例数量的极度倾斜的数据集上,AUC of ROC 可能失真。在这种情况下,PR-Curve 能够更好地反映出模型的性能。
点击率预估模型中的 AUC 与 gAUC(grouped AUC)
在个性化推荐、广告中,用作 rank 的模型,通常是点击率预估模型。此类模型将问题抽象为一个二分类问题,用模型预测用户是否会点击一个物品(推荐的内容或者广告)。由于该场景的目标是对物品进行排序,所以天然适合使用 AUC 作为评价指标。
但这有一个问题,我们通过例子来说明。
假设样本集中有 A 和 B 两个用户,分别都有 10 个物品。在这分别的 10 个物品当中,又分别有 5 个正例和 5 个负例。我们将这些正例和负例记为 A+/B+/A-/B-。假设将点击率预估模型的输出从高到低排序,结果是 A+/A-/B+/B-。此时,将两个用户的正负例混合起来看,AUC 不会很高。因为模型将部分负例(A-)排在了部分正例(B+)之前。但是,对于 A 和 B 分别来说,他们能观察到的正例均排在负例之前。也就是说,此时 AUC 不高,但实际效果很好。
这个问题可以这样解释:在模型预测分数越集中的区域,用户之间的细微差异导致的正负样本差异的影响就越大。因此,AUC 在这些区域可能会失真。此时,引入分组 AUC(grouped AUC, gAUC)可以缓解这一问题。
$$\text{gAUC} := \frac{\sum_{i = 1}^{n}(\omega_{i}\cdot\text{AUC}_{i})}{\sum_{i = 1}^{n}\omega_{i}}.$$
这里,$\text{AUC}_{i}$ 表示第 $i$ 个分组内的 AUC;$\omega_{i}$ 则表示该组权重。对于点击率预估的场景,每个用户对应一个分组,该用户的权重可设为该用户在样本集当中可见的曝光数量。即有
$$\text{gAUC} := \frac{\sum_{i = 1}^{n}(\#\text{impression}_{i}\cdot\text{AUC}_{i})}{\sum_{i = 1}^{n}\#\text{impression}_{i}}.$$


