动态规划与状态机：最大子序列和问题的扩展

前作以最大子序列和问题为起点，引出了动态规划思想的核心框架。今日恰逢构建之法群里，讨论起一个股票买卖问题，我用动态规划解决了。和邹欣老师的交流中，我进一步发现，引入状态机后，实际上股票买卖问题是最大子序列和问题的扩展。并且，这样的扩展可以更进一步地接近动态规划的核心，因此续作此篇，讨论一下动态规划与状态机。

动态规划与状态机

状态机是一种抽象的数学模型。它描述的是一些特定的状态，以及在这些状态之间转移的行为。如果状态的数量和转移方式都是有限的，那么这就是一个有限状态机。下图是一个有限状态机的示例：

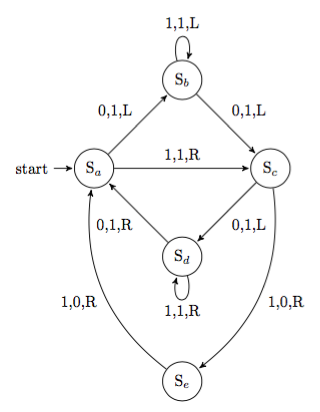
图中，每一个圆圈代表一个状态；每一道箭头代表一次转移；箭头上的内容则是转移的条件。

在前作中，我们讨论了动态规划思想的核心框架，其中提到了阶段、状态和最优子结构等概念。仔细琢磨这些概念，我们就能发现，他们和状态机中的概念是能够对应起来的：

状态机	动态规划
阶段	状态的集合
状态	状态
转移	从一个阶段到下一个阶段
转移条件	最优子结构

唯一的区别在于，动态规划只关注每个阶段的局部最优解；而状态机理论中，则没有这种倾向。

可见，动态规划思想，实际上是一种特殊的状态机罢了。

再探 Kadane 算法

那么，在最大子序列和的 Kadane 算法中，蕴含了怎样的状态机呢？呃，好吧。这个状态机非常简单，所以可能很多人都意识不到。

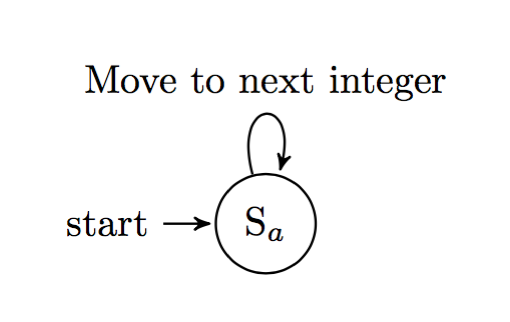
没错，就只有一个状态点而已。

start：读入序列中第一个整数
$\text{S}_a$：以当前整数为结尾的子序列之和
- 最优解：上述和中最大的那个
转移：读入下一个整数
最优解的转移条件（最优子结构）：local_max = max (local_max + nums[i], nums[i])

不难发现，代码中的循环，实际上就是实现了这个状态机而已。

股票买卖问题

接下来我们看一个最大子序列和的升级版问题：股票买卖问题。

这个问题是说：
给定一个包含若干整数（正负不限）的序列，该序列中的数值对应过去某天的股票价格。假设只有一张股票可以买卖，你可以自由地选择在某天买入或卖出，但必须保证：先买入后卖出、卖出后至少一天不允许交易（cooldown day）、每天最多只能交易一次（要么买入、要么卖出、要么不交易）。现在请问，在买入卖出的过程中，你最多能挣取多大收益？

假设我们对如下序列做讨论：

1	prices = [1, 2, 3, 1, 1, 2, 5, 3, 4, 2]

对于这个问题，我们可以定义如图所示的状态机：

这个状态机是对问题的忠实还原：

两个 start 表示最开始你可以选择休息，也可以选择购买股票。
买入股票后，进入状态 $\text{S}_1$，此时可以选择休息，或者卖出股票进入状态 $\text{S}_2$。
卖出股票后，进入状态 $\text{S}_2$，此时只能选择休息（cooldown day）进入状态 $\text{S}_0$。
进入状态 $\text{S}_0$ 后，可以选择继续休息，也可以选择买入股票。

我们要做的事情有两件：1. 定义初始状态；2. 找到在状态转移过程中，状态最优解之间的关系。

这很好做，因为我们有状态机作为参考。

对于 $\text{S}_0$ 状态来说，如果第一天不做操作，那么收益为 0，即 s0[0] = 0。接下来考虑，如果第 i 天进入了 $\text{S}_0$ 状态，那么第 i - 1 天要么在 $\text{S}_0$ 状态，要么在 $\text{S}_2$ 状态。因此 s0[i] = max (s0[i - 1], s2[i - 1])。

对于 $\text{S}_1$ 状态来说，如果第一天买入股票，那么收益为 -prices[0]，即 s1[0] = -prices[0]。接下来考虑，如果第 i 天进入了 $\text{S}_1$ 状态，那么第 i - 1 天要么在 $\text{S}_0$ 状态，要么在 $\text{S}_1$ 状态。因此 s1[i] = max (s0[i - 1] - prices[i], s1[i - 1])。

对于 $\text{S}_2$ 状态来说，不存在第一天就卖出的现象，因此我们需要一个足够小的值，来表示这种不可能出现的状态，即 s2[0] = -sys.maxint - 1。接下来考虑，如果第 i 天进入了 $\text{S}_2$ 状态，那么第 i - 1 天必然在 $\text{S}_1$ 状态。因此 s2[i] = s1[i - 1] + prices[i]。

于是，我们很容易能写出代码：

maxProfit.py

import sys

def maxProfit (prices):
    length = len (prices)
    if length < 2:
        return 0

    s0, s1, s2          = [0] * length, [0] * length, [0] * length
    s0[0], s1[0], s2[0] = 0, -prices[0], -sys.maxint - 1

    for i in xrange (1, length):
        s0[i] = max (s0[i - 1], s2[i - 1])
        s1[i] = max (s0[i - 1] - prices[i], s1[i - 1])
        s2[i] = s1[i - 1] + prices[i]

    return max (s0[-1], s2[-1])

if __name__ == "__main__":
    test_cases = [[], [1], [1, 2, 3, 1, 1, 2, 5, 3, 4, 2],
                    [6, 5, 4, 3, 2, 1, 0]]
    for prices in test_cases:
        print "The maxProfit of", prices, "is", maxProfit (prices)

结果输出：

The maxProfit of [] is 0
The maxProfit of [1] is 0
The maxProfit of [1, 2, 3, 1, 1, 2, 5, 3, 4, 2] is 6
The maxProfit of [6, 5, 4, 3, 2, 1, 0] is 0

符合预期；并且，由于循环内的操作均可以在常数时间内完成，因此这是一个 O(n) 复杂度的算法。