最近在自如租房时,负责租房的管家提供了名为「自如分期」的房租付款方式。观其操作模式,与信用卡分期还款、银行现金贷基本无差。印象里,以前有看到过文章讲述信用卡分期还款是不划算的;所以,在选择付款方式时,我就多留了一个心眼。
这里,将相关的分析,记录下来。以便让后来者明白:为什么说信用卡分期还款是不划算的。
利息和利率
利息和利率是大家都很熟悉的概念,但是对此二者深入思考的人恐怕不多。为了给读者树立利息的意义,此处我们给出一个抽象的表述:利息(或贴现)度量了资金在时间上积累的价值。
具体是什么意思呢?我们考虑,利息是负债方在还债时向债权方额外支出的费用;因此,负债方实际上是用利息向债权方「购买」了本金在一定时间内的流动性(使用权)。这就是说,利息实际上度量了债权方借出的本金在这段时间内积累的价值。
举例来说,Alice 作为债权方向负债方 Bob 借出 1,000 元,双方约定一年期后,Bob 以 10% 的利率一次性还清本息。那么,一年后,Alice 就会收到 1,100 元。
| 时间 | Alice | Bob | Bob 的借款本金 |
|---|---|---|---|
| 借出前 | 1,000 | 100 | 0 |
| 借出后 | 0 | 1,100 | 1000 |
| 一年后 | 1,100 | 0 | 0 |
单利与复利
在上一节的例子当中,Alice 和 Bob 约定的借款周期是一年,只有一次计息。因此,在上一节的例子当中,不存在单利与复利的分别。这一节,我们介绍单利和复利的分别,以及和收息方式的联系。
所谓单利,指的是在多轮计息的过程中,每次计息的本金保持不变;而复利指的是,在多轮计息的过程中,前次计息产生的利息,作为下一次计息的本金。可以想见,复利的计息方式在长时间积累之下,会产生远高于单利的利息。因此,复利又被称为「利滚利」或「驴打滚」,以形容其在长时间积累之下的可怕「威力」。
我们先来看单利的情况。Alice 作为债权方向负债方 Bob 借出 1,000 元,双方约定借款 3 年,每年年末 Bob 按 10% 的利率向 Alice 支付利息,第 3 年年末还清本金。这样一来,我们有:
| 时间 | Alice | Bob | Bob 的借款本金 |
|---|---|---|---|
| 借出前 | 1,000 | 300 | 0 |
| 借出后 | 0 | 1,300 | 1,000 |
| 一年后 | 100 | 1,200 | 1,000 |
| 两年后 | 200 | 1,100 | 1,000 |
| 三年后 | 1,300 | 0 | 0 |
由于 Bob 每年都向 Alice 支付借款利息,因此每年计息时,本金都是 1,000 元。因此,Bob 每次向 Alice 支付的利息,都是 $1000 * 10\% = 100$ 元。
接下来,我们来看复利的情况。Alice 作为债权方向负债方 Bob 借出 1,000 元,双方约定借款 3 年,每年年末按 10% 的利率计算利息并计入本金,第 3 年年末一次性还清本金利息。这样一来,我们有:
| 时间 | Alice | Bob | Bob 的借款本金 |
|---|---|---|---|
| 借出前 | 1,000 | 331 | 0 |
| 借出后 | 0 | 1,331 | 1,000 |
| 一年后 | 0 | 1,331 | 1,100 |
| 两年后 | 0 | 1,331 | 1,210 |
| 三年后 | 1,331 | 0 | 0 |
由于每年计息 10% 后计入下一周期的本金,故此 Bob 的借款本金逐年上升。这样一来,三年之后,Bob 总共需要向 Alice 支付 $1000 * (1 + 10\%)^{3} - 1000 = 331$ 元的利息。
在这一节的两个例子当中,Alice 和 Bob 的借贷关系均维持 3 年,借贷利率均为 10%;仅因为还款、计息的方式不同,导致了单利和复利的差别,最终导致 Bob 支付利息总额的区别。由此可见,收息方式会影响利息的计算方式,并影响最终的利息总额。在日常金融生活中,我们应当特别注意收息方式对资金运转的影响。
在大多数的金融活动中,都能看见复利的影子;相对来说,在真实的金融生活中,单利使用得较少。当然,这不是说单利就不存在了。据我了解,一些银行的消费类贷款,就是以单利做计算的:负债方定期向债权方支付等额的利息,到期后归还最后一期利息和全部本金。
计息周期与利率
在上一节的例子当中,Alice 和 Bob 约定的计息方式和利率均以「年」为单位计算。在实际生活当中,利率常以年计算,但计息周期往往不为整一年。例如,在下面这个例子中,计息周期为三月:Alice 作为债权方向负债方 Bob 借出 1,000 元,双方约定借款 1 年,利率为 12%,每 3 月计息一次,到期后一次性付清所有本息。这样一来,我们有:
| 时间 | Alice | Bob | Bob 的借款本金 |
|---|---|---|---|
| 借出前 | 1,000 | 125.5 | 0 |
| 借出后 | 0 | 1125.5 | 1,000 |
| 3 月后 | 0 | 1125.5 | 1,030 |
| 6 月后 | 0 | 1125.5 | 1,060.9 |
| 9 月后 | 0 | 1125.5 | 1,092.73 |
| 一年后 | 1125.5 | 0 | 0 |
这里,具体的计算过程如下:
- 年利率为 12%,那么 3 个月的利率为 3%;
- 按利率 3% 计息 4 个周期,本息合计
$1000 * (1 + 3\%)^{4} \approx 1125.5$元。
我们知道,若按第一节中的还款方式,Bob 只需在年末还给 Alice $1000 * (1 + 12\%) - 1000 = 120$ 元的利息。如此,我们仅仅改变了计息周期(从一年改为一季度),Bob 就不得不还给 Alice $125.5$ 元的利息。这样算下来,实际上 Bob 承担了 12.55% 的年利率。
由此,我们引出了名义利率和实际利率的关系。设债权方向负债方借出本金 $P$,约定名义年利率为 $r$,年计息 $n$ 次,则一年后本息合计为
$$F = P \cdot \Bigl(1 + \frac{r}{n}\Bigr)^n,$$
实际利率为
$$i = \Bigl(1 + \frac{r}{n}\Bigr)^n - 1.$$
不难看出,当 $n = 1$ 时,名义利率即为实际利率;当 $n > 1 $ 时,名义利率小于实际利率;当 $n < 1$ 时,名义利率大于实际利率。
在现实生活中,约定的利率默认都是名义利率。
时间上积累的价值
至此,我们已经见过了了利息、利率、单利、复利、计息周期、名义利率、实际利率等概念。若是没有提纲挈领的领悟,想必是挺令人犯恶心的。因此,这一节做一个小结——回到刚开始时的说明:利息(和贴现)度量了资金在时间上积累的价值。
在第一节的例子中,Alice 将 1,000 元钱借出给 Bob 一年。因此,Alice 丧失了这 1,000 元在接下来一年中的流动性。作为补偿/报酬,Bob 在一年后按约定给 Alice 100 元的利息。这 100 元的利息,即是 Alice 借出的 1,000 元在一年时间内积累下来的价值。
在第二节的单利的例子中,由于 Bob 每年都向 Alice 支付利息,也就是每年都补偿了 Alice 借出的 1,000 元在经历的这一年的时间积累的价值,因此每年只需要支付 100 元的利息。这就是单利的实质。
在第二节的复利的例子中,由于 Bob 直到最后一年才一次性还清本息;所以,Bob 本应在第一年年末支付的 100 元利息并没有支付,这就相当于 Bob 在第一年年末又向 Alice 借款 100 元。这样一来,原始的 1,000 元本金在第二年产生 100 元利息;新借的 100 元在第二年产生 10 元利息。加起来,第二年一共产生 110 元利息。以此类推,就变成了复利的模样。这就是复利的实质——每个周期的利息也要在时间上积累产生价值。
第三节介绍计息周期的例子和第二节的复利的例子是类似的。
这样一来,不论是利息多少、怎样计息、计息周期如何,我们都能得到统一的规律:利息系统是公平的,负债人应当支付的利息,等同于他在计息周期起始时应当偿还的金额(本金)在计息周期中积累的价值。简单来说就是:欠多少钱,计多少利息。
理解这个规律之后,接下来的内容就能以此提纲挈领了。
等额本金和等额本息
接下来,我们进入更加复杂的领域,两种不同的还款方式:等额本金和等额本息。
在上述所有例子当中,Bob 归还本金都是在约定时间末期一次性归还的。然而,在现实生活中,例如购房贷款都不是这样操作的。事实上,更多的借贷还款,每次还款都同时要偿还本金和支付利息。于是,按照不同的需求,就产生了两种还款方式。
等额本金
第一种还款方式是等额本金。这种还款方式一如其名:每次还款中,本金部分保持等额。也就是说,假设 Alice 作为债权方向负债方 Bob 借出 1,200 元,约定年利率 12%,按月计息;Bob 以等额本金的方式分 12 期还款。那么,Bob 每个月还款中本金部分是相等的,均为 $1200 / 12 = 100$ 元。这样一来,我们有
| 时间 | Bob 剩余应还本金 | Bob 本期应还利息 | Bob 本期应还本息合计 |
|---|---|---|---|
| 借款后 | 1,200 | 0 | 0 |
| 1 月后 | 1,100 | 12 | 112 |
| 2 月后 | 1,000 | 11 | 111 |
| 3 月后 | 900 | 10 | 110 |
| 4 月后 | 800 | 9 | 109 |
| 5 月后 | 700 | 8 | 108 |
| 6 月后 | 600 | 7 | 107 |
| 7 月后 | 500 | 6 | 106 |
| 8 月后 | 400 | 5 | 105 |
| 9 月后 | 300 | 4 | 104 |
| 10 月后 | 200 | 3 | 103 |
| 11 月后 | 100 | 2 | 102 |
| 一年后 | 0 | 1 | 101 |
| 合计 | N/A | 78 | 1278 |
这样的还款方式是符合我们之前所说的「欠多少钱,计多少利息」的。例如说,8 个月后的还款,因月利率是 1%,而 7 个月还款后尚欠款 500 元本金,故此 8 个月后的还款应当还本金 100 元以及利息 5 元,共 105 元。
对于这种还款方式,由于剩余应还本金呈等差序列下降,所以每期归还的利息也呈等差序列下降;这样一来,每次还款的金额也就呈等差序列下降;但是每期还款之中的本金部分是相等的。
这样一来,假设总借款额度为 $P$,年利率为 $r$,年计息 $n$ 次,分 $k$ 个计息周期还款,则第 $i$ 次还款应还的额度为
$$F_i = \frac{P}{k} + \Bigl(1 - \frac{i - 1}{k}\Bigr)\cdot P\cdot \frac{r}{n},$$
总计应还款额度为
$$F = P\cdot \Bigl(1 + \frac{r}{n}\cdot\frac{k + 1}{2}\Bigr),$$
总计应还的利息为
$$I = P\cdot\frac{r}{n}\cdot\frac{k + 1}{2}.$$
等额本息
与等额本金相对,还有一种还款方式是等额本息。本息合计即为应还款的总额,因此等额本息还款方式每次还款的金额是相等的。相比等额本金,等额本息的计算稍微复杂一些。
假设总借款额度为 $P$,年利率为 $r$,年计息 $n$ 次,分 $k$ 个计息周期还款,每次还款金额为 $X$,则第 $i$ 次还款后,尚欠款为
$$P_i = P_{i - 1}\Bigl(1 + \frac{r}{n}\Bigr) - X = P\Bigl(1 + \frac{r}{n}\Bigr)^{i} - X\cdot \sum_{j = 0}^{i - 1}\Bigl(1 + \frac{r}{n}\Bigr)^{j}.$$
这样一来,有
$$P_k = P_{k - 1}\Bigl(1 + \frac{r}{n}\Bigr) - X = 0,$$
也就是
$$P\Bigl(1 + \frac{r}{n}\Bigr)^{k} - X\cdot\frac{(1 + \frac{r}{n})^{k} - 1}{\frac{r}{n}} = 0.$$
这样一来,每次还款的金额为
$$X = P\cdot\frac{\frac{r}{n}\cdot(1 + \frac{r}{n})^{k}}{(1 + \frac{r}{n})^{k} - 1},$$
以及总的利息是
$$I = P\cdot \biggl(k\cdot\frac{\frac{r}{n}\cdot(1 + \frac{r}{n})^{k}}{(1 + \frac{r}{n})^{k} - 1} - 1 \biggr).$$
因此,假设 Alice 作为债权方向负债方 Bob 借出 1,200 元,约定年利率 12%,按月计息;Bob 以等额本息的方式分 12 期还款。那么,Bob 每个月还款额是相等的,均为 106.62 元。这样一来,我们有
| 时间 | Bob 剩余应还本金 | Bob 本期应还利息 | Bob 本期应还本息合计 |
|---|---|---|---|
| 借款后 | 1,200 | 0 | 0 |
| 1 月后 | 1,105.38 | 12.00 | 106.62 |
| 2 月后 | 1,009.81 | 11.05 | 106.62 |
| 3 月后 | 913.29 | 10.10 | 106.62 |
| 4 月后 | 815.80 | 9.13 | 106.62 |
| 5 月后 | 717.34 | 8.16 | 106.62 |
| 6 月后 | 617.89 | 7.17 | 106.62 |
| 7 月后 | 517.45 | 6.18 | 106.62 |
| 8 月后 | 416.00 | 5.17 | 106.62 |
| 9 月后 | 313.54 | 4.16 | 106.62 |
| 10 月后 | 210.06 | 3.14 | 106.62 |
| 11 月后 | 105.54 | 2.10 | 106.62 |
| 一年后 | 0 | 1.06 | 106.62 |
| 合计 | N/A | 79.44 | 1279.44 |
在计算的过程中,我们也遵循了之前所说的「欠多少钱,计多少利息」的规律。因此,不论是等额本息还是等额本金,在利率确定的情况下,以「资金在时间上积累是有价的」这个角度,两种还款方式是等价的。
然而,我们也应当注意到,等额本息方式还款的总利息要高于等额本金;但等额本金方式还款初期的每期还款额较高。这两个现象在贷款额度大、还款期限小时表现得特别明显。因此,在实际生活中,具体选用哪种还款方式,要根据具体的资金情况来决定。
信用卡分期还款
这里我们以招商银行信用卡分期还款的 12 期版本为例。按照招行的宣传,分期还款无利息,但是要收取每期 0.66% 的手续费。很多人会将这 0.66% 的手续费率理解为实际月利率,从而计算名义年利率为 7.92%。但这是个坑。
为方便对比,我们仍以 1,200 为例。以下是我尝试在招商银行掌上生活 App 中为 1,200 元进行 12 期信用卡分期付款的截屏。
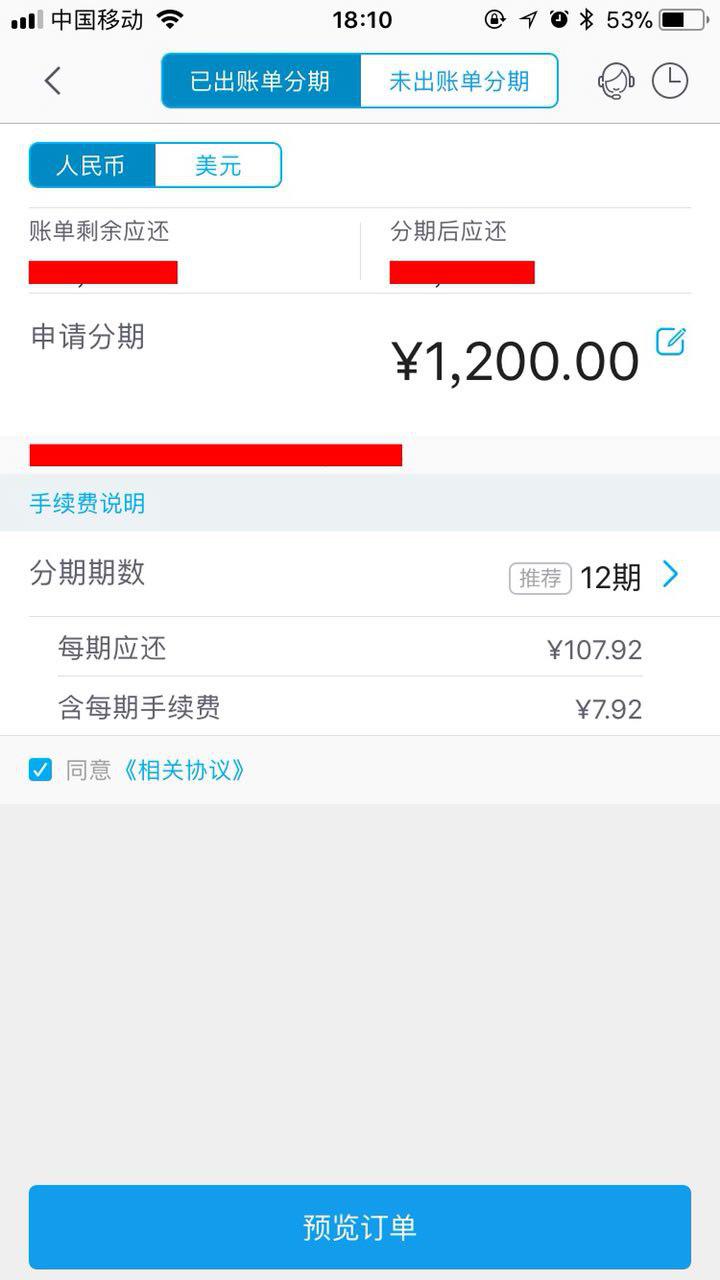
从截屏中,我们不难看到:
- 分期总额为 1,200 元;
- 分 12 期;
- 每期还款 107.92 元;
- 每期还款包含手续费 7.92 元。
乍一看,这应该是类似「等额本息」的还款方式。但是其实不然,因为,若按照真正的等额本息还款,每期还款额应该是 106.62 元,而不是 107.92 元。猫腻就藏在这里了。我们将还款记录如下
| 时间 | 剩余应还本金 | 本期应还利息 | 本期应还本息合计 |
|---|---|---|---|
| 借款后 | 1,200 | 0 | 0 |
| 1 月后 | 1,100 | 7.92 | 107.92 |
| 2 月后 | 1,000 | 7.92 | 107.92 |
| 3 月后 | 900 | 7.92 | 107.92 |
| 4 月后 | 800 | 7.92 | 107.92 |
| 5 月后 | 700 | 7.92 | 107.92 |
| 6 月后 | 600 | 7.92 | 107.92 |
| 7 月后 | 500 | 7.92 | 107.92 |
| 8 月后 | 400 | 7.92 | 107.92 |
| 9 月后 | 300 | 7.92 | 107.92 |
| 10 月后 | 200 | 7.92 | 107.92 |
| 11 月后 | 100 | 7.92 | 107.92 |
| 一年后 | 0 | 7.92 | 107.92 |
| 合计 | N/A | 95.04 | 1295.04 |
不难发现,在这样一个还款记录表中,剩余应还本金如同等额本金一样,呈等差序列逐渐下降;然而应还本息合计却如等额本息一样,保持不变。这样一来,相当于变相提高了年化利率。
那么,这种还款方式的实际利率是多少呢?我们说,利率的计算,应当本着「欠多少钱,计多少利息」的原则。纵观整 12 次还款,平均下来每期的应还本金为 650 元。因此,平均月利率为 $7.92 / 650 = 1.22%$;换算下来,年化利率就应该是 $1.22% * 12 = 14.62%$。
这是一个相当高的利率了,与宣传的 7.92% 相去甚远。因此,我们说,信用卡分期还款是非常不划算的。
按公式记录如下:假设总分期金额为 $P$,每次付款的手续费率占总分期金额的比例是 $r$,共分期 $k$ 次,那么实际利率应该是:
$$\frac{2k^{2}r}{k + 1} \times 100\%.$$
例如,在我们的例子当中,计算如下:
$$\frac{2\times 12^{2}\times 0.66\%}{13} \times 100\% \approx 14.62\%. $$
当然,我们必须承认,信用卡分期还款的方式也确实为我们提供了一种新的资金运转思路。在一些特定的情况下,选择分期还款也可以是一种不错的方式;但这就需要我们足够清醒,能够具体分析自己的财务状况和未来规划之间的平衡了。
特别地,自如提供的一些房子,月付和季付的价格是不同的:通常月付的价格会比季付高出不少;但是,使用自如分期,则能以季付的价格进行分期总价的计算;同时自如分期还会在服务费上有一定的优待。因此,在长期来看,若不在乎因分期带来的总价增长,同时却无法在短期内承受一次性支出季付价格,那么选择自如分期就是不错的方案。


