拉格朗日乘数法是约瑟夫·拉格朗日(Joseph-Louis Lagrange)提出的关于多元函数在有若干等式约束条件情况下求解最优化问题的解法。由于它在最大熵模型中有应用,所以在谈最大熵模型之前,首先要讲讲拉格朗日乘数法。
最简情形下的拉格朗日乘数法
描述
现在假设说有自变量 $x$ 和 $y$,以及关于它们的二元函数 $f(x, y)$,另有关于它们的等式约束条件 $g(x, y) = c$。现在的问题是,求解函数 $f$ 在约束条件 $g = c$ 下的最大值或最小值。显然,这是一个最优化问题,可简记为(以求最大值为例)
$$ \begin{aligned} &{}\max f(x, y), \\ &{}\text{s.t. } g(x, y) = c. \end{aligned} $$
拉格朗日乘数法是说,上述问题可转化为求解拉格朗日函数在无约束条件下的极值求解问题,
$$ \mathcal{L}(x, y, \lambda) \overset{\text{def}}{=}f(x, y) + \lambda\cdot g(x, y). $$
亦即求解拉格朗日函数驻点的问题
$$ \begin{cases} \frac{\partial \mathcal{L}}{\partial x} = 0, \\ \frac{\partial \mathcal{L}}{\partial y} = 0, \\ \frac{\partial \mathcal{L}}{\partial \lambda} = 0. \end{cases} $$
这是关于 $x$, $y$ 和 $\lambda$ 的方程组,而它的解可能不止一个。拉格朗日乘数法说明,原优化问题的解必然处于该方程组的解集之中,只需对比解集中的点 $(x, y)$ 在原函数 $f(x, y)$ 中的值,即可得到原函数在等式约束条件下的最值。
证明
拉格朗日乘数法的证明不难,简单(并不完全严格但足以说明问题)证明如下:
设二元函数 $f(x, y)$ 在点 $(x_0, y_0)$ 处有极值 $\kappa$,并且在点 $(x_0, y_0)$ 的领域内连续,则在点 $(x_0, y_0)$ 处有
$$f(x_0, y_0) = \kappa.$$
另有一作为等式约束条件的常值函数 $g(x, y) = c$。显然,两个函数在点 $(x_0, y_0)$ 处的全微分有
$$ \begin{aligned} \mathrm{d}f =&{} \frac{\partial f}{\partial x}\mathrm{d}x + \frac{\partial f}{\partial y}\mathrm{d}y = 0, \\ \mathrm{d}g =&{} \frac{\partial g}{\partial x}\mathrm{d}x + \frac{\partial g}{\partial y}\mathrm{d}y = 0. \end{aligned} $$
考虑微分 $\mathrm{d} x$ 和 $\mathrm{d}y$ 是任意的无穷小量,故两个方程关于两个微分的系数应当成比例。这就是说
\begin{equation} \begin{cases} \frac{\partial f}{\partial x} - \lambda\cdot\frac{\partial g}{\partial x} = 0, \\ \frac{\partial f}{\partial y} - \lambda\cdot\frac{\partial g}{\partial y} = 0. \end{cases}\tag{*}\label{star} \end{equation}
二式相加并积分即得拉格朗日函数
$$ \mathcal{L}(x, y, \lambda) \overset{\text{def}}{=}f(x, y) + \lambda\cdot g(x, y). $$
这也就是说,原优化问题的解必然是拉格朗日函数的一个极值。
物理意义
考虑函数 $f(x, y) = d$ 的图像。由于只有一个自由度,所以它是一条曲线。特别地,对于序列 $\bigl\{d_1, d_2, \ldots\bigr\}$ 来说,$f(x, y) = d_k$ 形成了一系列的曲线。若将 $d_k$ 理解为高度,则这一系列的曲线即是函数 $f(x, y)$ 的等高线组。同样,对于约束 $g(x, y) = c$ 来说它也是一条曲线,我们称之为约束曲线。
据此,可绘图如下(摘自英文 Wikipedia)
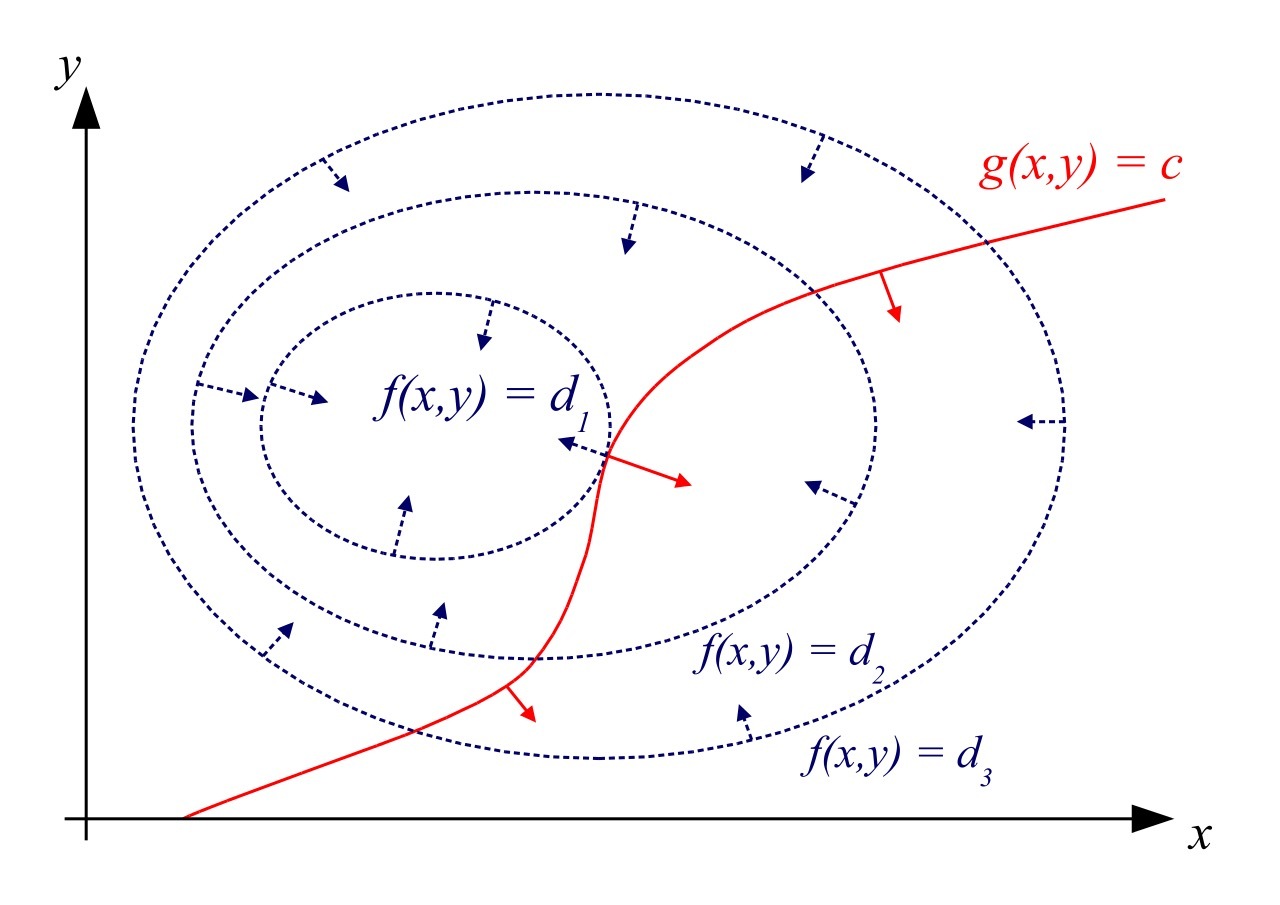
现在我们需要思考的是,等高线组和约束曲线满足什么条件时,我们可以说函数 $f$ 在条件 $g = c$ 的约束下取得极值。不难理解,等高线组中的一条等高线与约束曲线相切时,函数 $f$ 可能取得极值。反过来想想就很容易理解了,假设不相切时(即相交时)取得极值,例如说在图中 $f(x, y) = d_2$ 时取得极值。如此,从交点开始沿着约束曲线的两个方向滑动,都还能继续与其它等高线相交,这与 $f(x, y)$ 取得极值矛盾。因此 $f(x, y)$ 在约束下取得极值时,函数曲线必然与约束曲线相切。
函数曲线相切,意味着两个函数的法线在切点重合,也就是两个函数的法向量相差一个系数 $\lambda$,这也就是说两个函数在切点的梯度向量相差一个系数 $\lambda$,即 $\Bigl(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\Bigr) = \lambda\Bigl(\frac{\partial g}{\partial x}, \frac{\partial g}{\partial y}\Bigr)$。这恰好是上述证明过程中的 (\ref{star})-式的向量表示。
因此我们说,拉格朗日乘数法有很直观的物理意义。
推广到一般情形下的拉格朗日乘数法
现在假设说有自变量向量 $x_1$, $x_2$, ..., $x_n$,以及关于它们的 $n$ 元函数 $f(x_1, x_2, \ldots, x_n)$,另有关于它们的一组等式约束条件 $\bigl\{g_j(x_1, x_2, \ldots, x_n) = c_j\bigr\}_K$。现在的问题是,求解函数 $f$ 在约束条件组 $\bigl\{g_j = c_j\bigr\}_K$ 下的最大值或最小值。它可以转化为求解拉格朗日函数在无约束条件下的极值求解问题,
$$ \mathcal{L}(x_1, x_2, \ldots, x_n, \lambda_1, \lambda_2, \ldots, \lambda_K) \overset{\text{def}}{=} f(x_1, x_2, \ldots, x_n) + \sum_{j = 1}^{K}\lambda_jg_j(x_1, x_2, \ldots, x_n). $$


