作为一个强迫症(OCD)患者,曾经我一直对随机梯度下降(Stochastic Gradient Descent)表示怀疑。毕竟,每次只选择少量样本计算梯度,这靠谱吗?强迫症患者心里泛起了浓浓的怀疑。然而经年的实践经验结合理论分析表明,强迫症患者也需要随机梯度下降。
这篇文章尝试尽可能用少的数学公式,讲一讲这个问题。
问题
这里讨论的梯度下降(Gradient Descent)和随机梯度下降,都是为了解决机器学习/深度学习当中模型训练中的优化问题而设计的。在机器学习/深度学习当中,模型的训练问题往往会被转换成求使得目标函数值最小的参数组合的最优化问题。具体来说是
$$\vec{\theta}^{*} = \mathop{\arg\min}_{\vec{\theta}}\text{Obj}\bigl(h(\vec x;\vec{\theta})\bigr).$$
这里,$h(\vec x;\vec{\theta})$ 是目标模型,其中 $\vec x$ 是输入特征向量,$\vec{\theta}$ 是模型的参数,$\text{Obj}(\cdot)$ 是目标函数。
在样本集给定时,可将 $\text{Obj}\bigl(h(\vec x;\vec{\theta})\bigr)$ 看做是 $\vec\theta$ 的函数——不妨将其记为 $f(\vec\theta)$,则我们的目标就是要找到该函数等高线中的最低谷位置对应的 $\vec\theta$ 的取值。
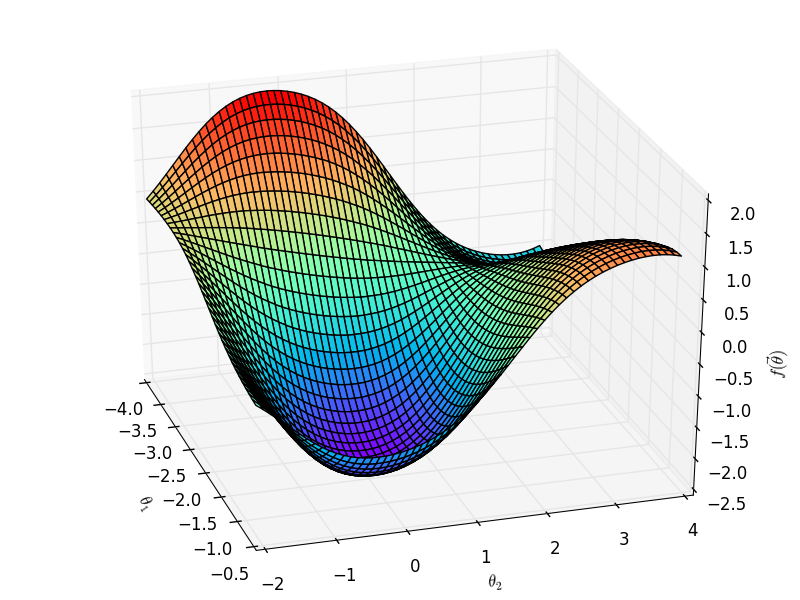
梯度下降
概述
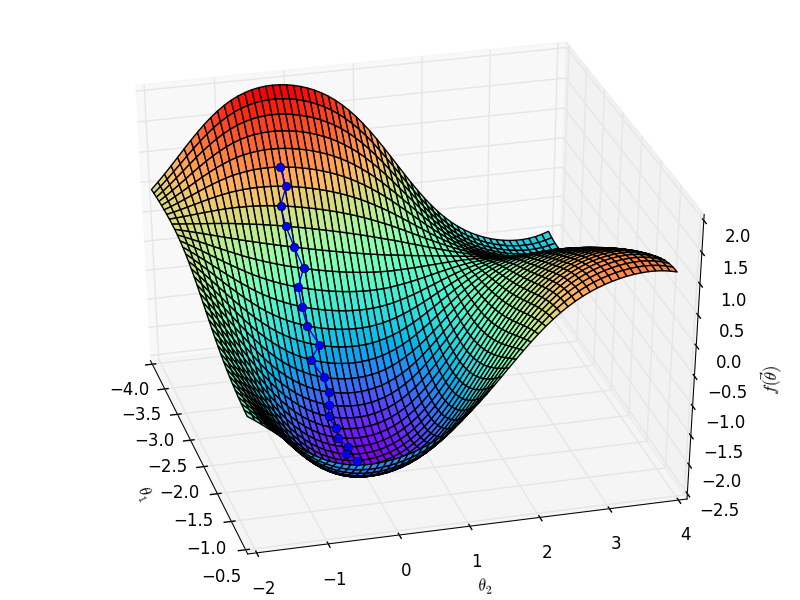
既然要找到目标函数的「山谷」,那我们就要想办法「下山」。在数学上,上升最快的方向是函数的梯度方向,于是梯度方向的反方向就是下降最快的方向。于是有参数更新
$$\vec \theta_{n + 1} \gets \vec\theta_{n} - \eta\nabla f(\vec\theta_{n}).$$
这里,$\vec\theta_{n}$ 是第 $n$ 轮迭代后的参数;$\nabla f(\vec\theta_{n})$ 则是第 $n$ 轮迭代后目标函数的梯度;$\eta$ 是学习率,也就是梯度下降的步长。
问题
梯度下降优美、清晰、明确。但梯度下降也有它的问题。
第一个问题是效率低。梯度下降法需要处理计算所有样本,而在工程中我们面对的样本集合往往非常大。这样一来,处理所有样本就会变得效率非常低,缓慢得不可接受。
第二个问题是缺乏跳出陷阱的能力。这里的陷阱指得是诸如鞍点、局部最优点之类的梯度为零的点。
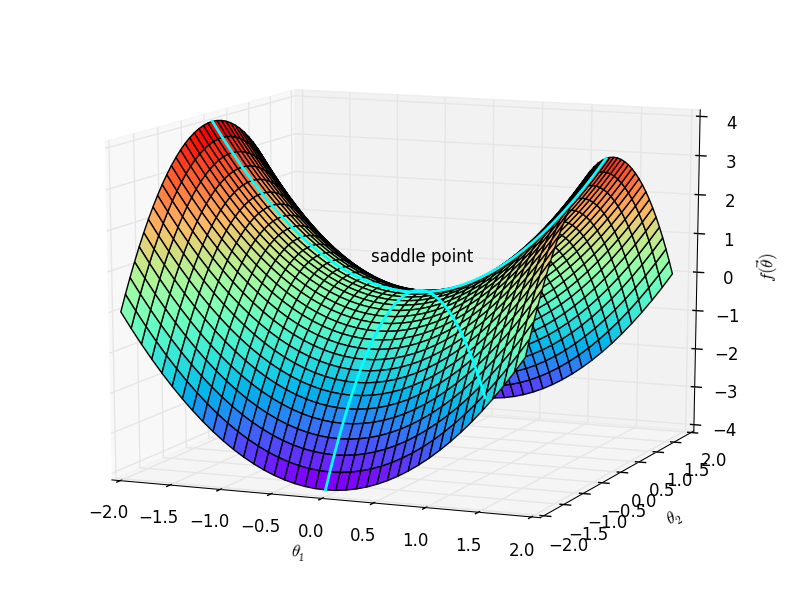
这是因为,当目标函数落入陷阱后,梯度为零。于是目标函数的参数再也无法更新,模型实质上收敛在不恰当的位置。
随机梯度下降
概述
随机梯度下降(Stochastic Gradient Descent,SGD)的表达式和梯度下降差别不大:
$$\vec \theta_{n + 1} \gets \vec\theta_{n} - \eta_ng_n.$$
这里,$g_n$ 是随机梯度。具体来说,它是用单个样本(而非所有样本)计算得到的梯度。在实践中,也可能是使用较小的集合(mini batch)计算得到的梯度。随机梯度满足
$$E[g_n] = \nabla f(\vec\theta_n).$$
这也就是说,尽管由于样本选择带来了一定的随机性,但在期望的角度,随机梯度是等于真实的梯度的。用等高线图来表示,随机梯度下降就像是喝醉了酒的梯度下降:它依稀认得路,最后也能自己走回家,但是走得歪歪扭扭。(黄色的是梯度下降的路线,绿色的是随机梯度下降的路线)
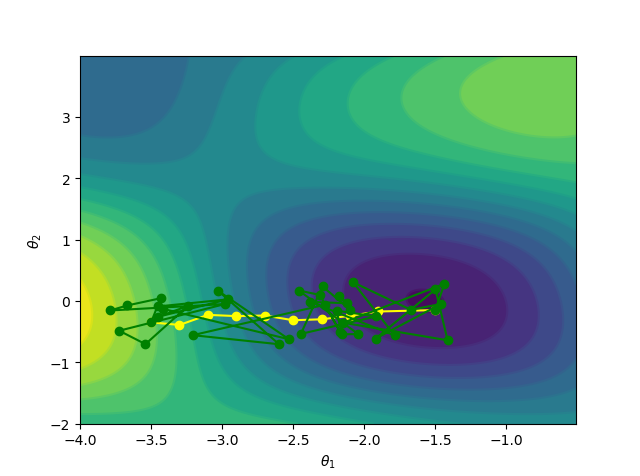
效率的提升
显而易见,随机梯度下降想要收敛,需要更多的迭代步骤。但是,由于每次只需要少量样本来计算随机梯度,实际上的效率会提升很多。试想,若训练数据集有 100 万个样本点,每次我们取其中的 100 个计算随机梯度。这样,在计算梯度的时候,效率就提升了 1 万倍。如此一来,哪怕多迭代几倍甚至十几倍,总体来说效率也是提升了。
效果的提升
虽然强迫症肯定会怀疑,随机梯度下降每次只用部分样本,这样的随机性和噪声靠谱吗?但实际上,哪怕梯度下降的训练时间比随机梯度下降多千百倍,但实际效果却远不如随机梯度下降得到的模型。
这里蕴含着两层含义:
- 随机梯度下降能很好地收敛;
- 随机梯度下降能收敛到更好的最优点上。
关于 (1),这里不打算展开来讲。但有大量的理论工作证明,在 $f$ 是凸函数的情况下,只要噪声不离谱,随机梯度下降都能很好地收敛。(2) 的性质实际上是在说 SGD 能够较好地逃离鞍点这类「陷阱」。为了说明这一点,首先要引入一个概念:strict saddle 函数。它是说,对于函数定义域内的任意一个点 $x$,满足:
- 函数在 $x$ 点的导数比较大(因而能够做梯度下降);或者,
- 函数在 $x$ 点附近有最小值(因而已接近完成优化任务);或者,
- 函数在 $x$ 点的二阶偏导组成的 Hessian 矩阵至少含有一个负的特征值(因而沿着这个方向能够滑下去,降低函数值)。
在机器学习/深度学习任务中,大多数用到的函数都满足(或者近似满足,虽然我不知道怎么证……)strict saddle 函数的定义。对于 strict saddle 函数,如果梯度下降遇到了鞍点,只需要在鞍点加扰动,能够顺着负的特征值方向滑下去降低函数值了。金驰菊苣 17 年的论文(How to Escape Saddle Points Efficiently)就说明了这一点:SGD 引入的扰动,能够在较大概率下逃离鞍点。文章证明的思路很巧妙,它首先证明了任意两个点在负特征值方向上的投影距离大于 $u / 2$,则其中至少有一个点能够通过有限步的 GD 迭代逃离鞍点。接下来,只需要通过 $u$ 计算出落入这一区间的概率下界,说明它足够小,就能说明 SGD 引入的扰动,能够在较大概率下逃离鞍点了。
总结
OCD 患者也需要 SGD,因为相对于 GD,它:
- 效率较高;
- 能够收敛;
- 能够收敛到更好的最优点上。
因最近工作较忙,这篇文章有些「虎头蛇尾」。实际上,这篇文章从三月中旬动笔至此已经两个多月了,可见其中受了多少打扰。拖延至今实不愿继续拖沓下去,因此本着「烂尾好过无尾」的想法(真不要脸),就这样草草结尾了。望各位看官见谅。


