先前我们从 LR 开始,讨论了因子分解机(FM)模型。FM 解决了稀疏数据场景下的自动特征组合问题,因而在广告、推荐等具有高维稀疏特征的领域被广泛使用。因其简单、可解释性强、效果好,FM 模型通常会被作为业务初期快速取得收益的首选。
这里将 FM 模型家族至今为止的演进做一个整理总结。
FM
首先回顾一下 FM 模型的预测函数。
$$\hat y = f(\vec x) = w_0 + \sum_{i = 1}^{n}w_ix_i + \sum_{0 < i < j <= n}\langle \vec v_i, \vec v_j\rangle x_ix_j.$$
这里 $n$ 是特征向量 $\vec x$ 的长度,即特征的维数。$v_i$ 是长度为 $k$ 的向量,与特征 id 对应,称为特征的隐向量。特征的隐向量是特征相互作用之后得到的抽象表征。经验来说,一般有 $k = \max\Big\{4, \big\lfloor\sqrt[4]{n}\big\rfloor\Big\}$。
在特征交叉方向上的改进
对 FM 的第一个改进方向是在特征交叉方向上去做改进。
FFM (Field-aware FM)
FFM 是 NTU(国立台湾大学)的 Yu-Chin Juan(阮毓钦,现在美国 Criteo 工作)与其比赛队员,借鉴了来自 Michael Jahrer 的论文中的 field 概念提出了 FM 的升级版模型。
$$\hat y = w_0 + \sum_{i = 1}^n w_i x_i + \sum_{0 < i < j <= n} \langle \vec {v}_{i, f_j}, \vec {v}_{j, f_i} \rangle x_i x_j.$$
相比 FM,FFM 为每个特征构造的不再是隐向量,而是隐矩阵;具体来说,是一个 $k$ 行 $F$ 列的矩阵。它由 $F$ 个 $k$ 维列向量组成;每个列向量 $\vec v_{i, f}$ 表示特征 $i$ 与其他所有第 $f$ 个 field 中的特征相互作用得到的抽象表征。式中 $f_i$ 表示第 $i$ 维特征所属 field 的 id。
从隐向量升级到隐矩阵,一方面带来的是参数量的增长(乘以 $F$ 倍)而在训练、预测时对内存产生更大压力,另一方面是无法如 FM 那样简化计算。因此它训练时的复杂度是非常高的。这使得它在各种竞赛中有所表现,但在实际业界应用有限。
AFM (Attentional FM)
AFM 是浙大(Jun Xiao, Hao Ye, Fei Wu)和新加坡国大(Xiangnan He, Hanwang Zhang, Tat-Seng Chua)几位同学提出来的模型。AFM 首先对 FM 做了神经网络改造,而后加入了注意力机制,为不同特征的二阶组合分配不同的权重。

$$\hat y = f(\vec x) = w_0 + \sum_{i = 1}^{n}w_ix_i + \sum_{0 < i < j <= n}\alpha_{ij}\big\langle \vec p, (\vec v_i \odot \vec v_j)\big\rangle x_ix_j.$$
这里,$\alpha_{ij}$ 是通过注意力机制学习得到的特征 $i$ 和特征 $j$ 组合的权重,$\vec p$ 是对隐向量每个维度学习得到的权重,$\vec v_i \odot \vec v_j$ 表示向量 $\vec v_i$ 和 $\vec v_j$ 逐项相乘得到的新向量。显然,当 $\alpha_{ij} \equiv 1$ 且 $\vec p = \vec 1$ 时,AFM 退化为标准的 FM 模型。
AFM 和 FFM 都是从「特征和不同特征进行组合时,表征应该稍有差异」这个点出发,尝试对 FM 进行改进的。FFM 是基于 field 的概念,使得特征对不同 field 里的特征采取不同的表征,同时特征对不同 field 特征里的表征互不关联。AFM 是基于 attention 机制的,对不同特征的表征仅有权重($\alpha_{ij}$)上的不同。从参数数量来说,AFM 会远小于 FFM。从这个角度说,AFM 在业界的应用前景应该比 FFM 更好。
FwFM (Field-weighted FM)
$$\hat y = f(\vec x) = w_0 + \sum_{i = 1}^{n}w_ix_i + \sum_{0 < i < j <= n}r_{f_if_j}\langle \vec v_i, \vec v_j\rangle x_ix_j.$$
这里 $r_{f_if_j}$ 是针对特征 $i$ 所属 field $f_i$ 和特征 $j$ 所属 field $f_j$ 学习的参数。
FwFM 改进的出发点与 FFM 和 AFM 相同,但吸取了 FFM 和 AFM 各自的优点。它相当于是 $\vec p = \vec 1$ 且 $\alpha_{ij}$ 简化为 $r_{f_if_j}$ 的 AFM。相对于 FFM,它改掉了用隐矩阵来 model field 的做法,而是用 $r_{f_if_j}$ 捕捉 field 的信息,因而大大降低了参数数量。
引入深度神经网络
对 FM 进行改进的第二个方向是引入深度神经网络。
DeepFM
DeepFM 的论文发表在 IJCAI 2017 上。它是在 Wide & Deep 框架上,将 LR 部分替换成了 FM,以增强 wide 部分对二阶交叉特征的捕捉能力。目前来说,它已被业界快速跟进和应用到推荐、广告、搜索等场景。
其实 Wide & Deep 框架才是这一改进的精髓。不难发现,除了将 FM 与 NN 拼起来得到 DeepFM,我们还可以将 FFM、AFM、FwFM 和 NN 拼起来得到相应的 DeepXFM 版本。但这样难免有水论文的嫌疑了……
NFM (Neural FM)
DeepFM 是用 Wide & Deep 框架,在 FM 旁边加了一个 NN,最后一并 sigmoid 输出。NFM 的做法则是利用隐向量逐项相乘得到的向量作为 MLP 的输入,构建的 FM + NN 模型。
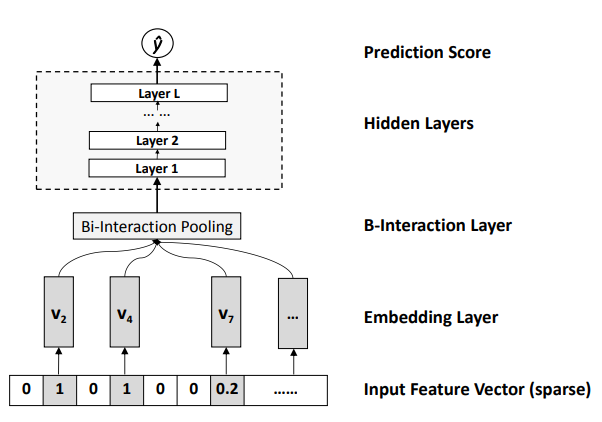
$$\hat y = f(\vec x) = w_0 + \sum_{i = 1}^{n}w_ix_i + f(\vec x).$$
如图所示的是上述第三项 $f(\vec x)$ 的结构。Embedding 层中的向量即是传统 FM 模型中的 $x_i\vec v_i$;Bi-interaction 池化层则是将特征两两交叉后,逐项向量相乘再做向量加法,即池化层的输出是一个与隐向量长度相同的向量:
$$\sum_{0 < i < j <= n} x_ix_j(\vec v_i \odot \vec v_j).$$
紧接着再以上述向量作为一个 $L$ 层的 MLP 的输入,接一个全链接的 MLP 而后输出。显然,和 AFM 中的情况类似,当 $L = 0$ 且输出层参数全为 $1$ 时,NFM 退化为原始的 FM 模型。
NFM 的复杂度是传统 FM 的复杂度与 MLP 的合。因此它与 DeepFM 的复杂度是相同的。
利用偏序概率,迁移到 rank 任务上
以前提到过 RankNet 的创新。通过引入偏序概率,我们可以把任何一个模型转变成 pairwise 的排序模型。
具体来说,对于待排序的 item $x_i$ 和 $x_j$,有模型的打分函数 $f$,从而求得得分 $s_i = f(x_i)$, $s_j = f(x_j)$,而后得到偏序概率
$$P_{ij} = P(x_i \rhd x_j) = \text{sigmoid}(s_i, s_j).$$
这样,我们就将排序问题中的偏序,转换成了二分类问题($x_i$ 是否应该排在 $x_j$ 之前)。之后只需要套用二分类问题的解法即可。
Pairwise FM
Pairwise FM 的做法就是如此。只需要将上述打分函数 $f$ 设为 FM 即可。
LambdaFM
和 LambdaMART 中的做法一样,若在 FM 的基础上,将梯度上辅以 $\Delta Z$ 作为 pair 的权重,则变成了 listwise 的排序算法。
其他魔改
上述三类对 FM 模型的改进,相对来说都有比较明确的方向。还有一些改进,在模型本身的角度没有形成特定的方向。但这些改进也有一些意义,因此罗列如下。
加入 FTRL 框架
FTRL 框架是一个在线学习框架。最早是 Google 提出来应用在 LR 上的。这篇发表在 KDD 2018 的文章将 FTRL 引入了 FM 模型。但这其实不是什么新鲜事,CastellanZhang 早在 2016 年就开源了相应的实现 alphaFM。
DFM (Discrete FM)
原始 FM 的隐向量是在实数空间的向量。虽然 FM 可经过数学变换将复杂度降低到线性(相对隐向量长度 $k$),但在某些场景,复杂度仍然很高。因此山东大学(Han Liu, Liqiang Nie)、新加坡国大(Xiangnan He, Fuli Feng)、电子科技大学(Rui Liu)和新加坡南洋理工(Hanwang Zhang)的几位同学提出了 DFM 模型。
$$\hat y = f(\vec x) = w_0 + \sum_{i = 1}^{n}w_ix_i + \sum_{0 < i < j <= n}\langle \vec b_i, \vec b_j\rangle x_ix_j.$$
它和原始 FM 模型唯一的差别是将隐向量从实数空间简化到 $\{-1, +1\}$。不难预见,效果相对 FM 会有一定下降。
RFM (Robust FM)
$$\hat y = f(\vec x) = w_0 + \sum_{i = 1}^{n}w_i(x_i + \mu_i) + \sum_{0 < i < j <= n}\langle \vec v_i, \vec v_j\rangle (x_ix_j + \Sigma_{jk}).$$
Robust 即是「鲁棒性」的那个英文单词。这一个改进的出发点是 FM 大量用于和用户反馈相关的场景(例如推荐、计算广告),而 FM 模型有一个隐含假设:用户的反馈都是真实的。RFM 认为这些反馈不一定都是真实的,因此加入用于捕捉随机噪声的 $\mu_i$ 和 $\Sigma_{ij}$ 两项。
从个人的判断来说,这种改进对 FM 的鲁棒性确实会有提升。但是,(也许是我孤陋寡闻)没有了解到业界有广泛的应用这一改进。猜测可能的原因是 $\Sigma_{ij}$ 项的加入破坏了原 FM 的数学变形,使得时间复杂度变成了 $\Theta(kn^2)$ 从而降低效率。
小结
近年来,针对原始 FM 的改进主要集中在三个方向:
- 细化二阶特征交叉的处理方式,以捕捉更多信息;
- 与 NN 结合,利用 NN 捕捉高阶交叉特征;
- 利用偏序概率,迁移到 rank 任务上去。
特别地,也有所谓的 High-order FM 的改进。但个人认为这种接法属于「脱裤子放屁」——NN 是公认地能够较好地捕捉高阶交叉特征的方法,再去魔改 FM 意义不大。
当然,在其他方向,也有一些改进。但这些改进目前未成体系,看起来也不容易在方向上成为一个流派。因此这些改进在本文中一律归到「魔改」的范畴中了。
希望本文能够让读者对 FM 的各种变体、改进有一个比较直观的认知。另祝 @turbo0628 同学生日快乐~


